ｗ さんの書込 (2005/08/26(Fri) 02:26)

（−電池＋）ていこう（−電池）←は1周してると考えて．矢印は電界 →→→→→→

↑の図だったら何も疑問は感じないのですが

（−電池＋）――――抵抗――――（−電池） ―は導線 →→→→→→→→→→→→

これだと電界が図のように広がってしまい，下のような疑問がでてくるのですが 電池の＋極を１０V，−極を０Vとおく．考えにくいので＋電荷が移動するとかんがえます． ＋電荷は最初１０Vのエネルギーをもって出発．進むにつれ電位を運動エネルギーに変換して加速する． 抵抗を通過するには電池の起電力１０Vを全てを加速につかわないといけないはずなのに，抵抗を 通過するときにはまだ電位１０Vをを全て運動エネルギーに変換しきってないのがおかしい気がするのですが？

FKD さんのレス (2005/08/26(Fri) 17:52)

No6543などで篠原さんが指摘されていることですが， 超伝導でもないかぎり導線の抵抗はゼロにはなりません． 教科書等で導線の抵抗をゼロと扱っているのはあくまで近似です． 抵抗の両端にかかる電圧は厳密には電池の電圧とは一致しません．

篠原 さんのレス (2005/08/26(Fri) 18:21)

もしかして，「導体」や「導線」と書くから，イメージしにくいのかもしれませんね． 抵抗値の異なる3つの抵抗が電源につながってると考えたらどうですか？？

電源(+)→抵抗(1Ω)→抵抗(10kΩ)→抵抗(1Ω)→電源(-)

電源電圧を10Vとすると，10kΩの抵抗での両端の電圧は9.998Vになります． どうですか？電源電圧と抵抗の電圧は0.002Vだけ違うことになりますよね？ でも，「電源電圧と抵抗の電圧はほとんど同じ」と言うこともできます． つまり，この場合は「導線の抵抗(1Ω)はほとんど無視できる」と言うことです．

ｗさん，納得していただけます？？

ｗ さんのレス (2005/08/26(Fri) 18:39)

レスありがとうございます．もし導線に抵抗があったとしても，普通導線部分のほうが，抵抗よりも長いですよね？導線のほうが抵抗よりも長いということは，それだけ電界をたくさん受けポテンシャルエネルギーを運動エネルギーに変換している（その運動エネルギーは熱となってなくなっているが）．ここまでが正しいとするなら，より運動エネルギーを必要とする抵抗よりも導線部分で運動エネルギーを消費してるのは明らかにおかしいですよね？

FKD さんのレス (2005/08/26(Fri) 18:52)

>導線のほうが抵抗よりも長いということは， >それだけ電界をたくさん受けポテンシャルエネルギーを >運動エネルギーに変換している この部分に少し誤解があります． 消費される単位時間あたりのエネルギー 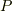は 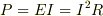です． No.6608の場合ですと 電流 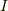の値は導線，抵抗ともに同じですから 消費されるエネルギーは抵抗の値に比例することになります．

#もちろん材質が同じなら抵抗は長さに比例します． #長さ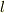を ,断面積を とすると #抵抗値 は 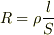となります． #ここで は材質に固有の比例定数（電気抵抗率）です．

ｗ さんのレス (2005/08/26(Fri) 19:42)

>>FKDさんへ 消費される熱エネルギーはその公式で正しいと思いますが，電位から運動エネルギーへの変換はどれだけ電界の力をうけたかによりませんか？

ｗ さんのレス (2005/08/26(Fri) 19:45)

↑のに少し追加です． W＝VIは正しいですが，導線では抵抗内よりもたくさんの電界を受け電位は運動エネルギーとなると自分は思うので，抵抗に到達したときには電位は下がってると思うのですがということです

篠原 さんのレス (2005/08/26(Fri) 19:58)

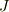( は電流密度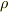， は抵抗率， は電界) この式は，オームの法則を示しているものなのです．

キルヒホッフの電流則によって，導体に流れている電流と抵抗に流れている電流が等しくなることは保証されます．

仮に，導体と抵抗の断面積が等しければ，導体と抵抗の電流密度 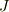は等しくなります． 導体の抵抗率は抵抗器の抵抗率よりかなり小さな値となるため，電流密度 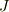が等しくなるためには，導体内の電界が抵抗内での電界よりかなり小さな値となるはずです．このため，導体内で電荷が電界より受け取るエネルギーは，抵抗内で受け取るエネルギーよりも小さな値となるはずです．

また，導線の距離が長くなった場合，導体内で受け取るエネルギーが確かに大きくなります．この場合は，その導線の距離の長さにより，導体の抵抗を無視できなくなった状態を表しています．

FKD さんのレス (2005/08/26(Fri) 21:20)

>導線では抵抗内よりもたくさんの電界を受け

そうはなりません． 導線両端の電位差が抵抗器両端の電位差よりも十分に小さいので 電界の大きさも導線内部の方が抵抗器内部と比べて小さくなります．(*) そして，その電位差は抵抗の大きさで決まるわけです．

*導線の長さはそれほど長くないとします

FKD さんのレス (2005/08/26(Fri) 21:38)

ちょっと調べたのですが，銅の抵抗率は0.00000001673[Ωm]だそうです． 断面積を1[mm^2]，長さを1[m]にしてもその抵抗は0.01673[Ω]です． とても小さいですね．

ｗ さんのレス (2005/08/26(Fri) 22:49)

＞＞篠原さん，FKDさんへ

とても分かりやすいです．感謝です． しかし，電界を発生してるものが電池の両極の＋，−の帯電なので，電界を導線では弱く抵抗では強くなんてｋとができるのでしょうか？

篠原 さんのレス (2005/08/26(Fri) 23:37)

「電界を発生してるものが電池の両極の＋，−の帯電なので」 この点は，あっているかどうか分かりませんが，通常，電気回路において帯電により電界が発生するとはあまり考えません． どちらかと言うと，電源により電位差が与えられる，と言う考えで，電気回路の問題を考えます．

「電界を導線では弱く抵抗では強くなんてことができるのでしょうか？」 実は，このあたりが，とおりすがりさんやkenさんが議論していることです． あっていると断言できませんが，私の考えを述べます．

ガウスの法則というものをご存知でしょうか？ かみ砕いて言うと，「電束密度が変化する場所では電荷が存在する」 もしくは，言い換えると，「電荷が存在する場所では電束密度が変化する」 というものです． 今考えている問題の場合，導体と抵抗体における電束密度が大きく違うことになります． このため，導体と抵抗体の界面において，電荷が存在しており，その電荷の影響により電束密度の差が発生し，電界に大きな違いが現れるのではないかと考えています．

今のところ，kenさんから明確な反論はありませんし，私はこれであっていると考えるのですが，「絶対あっている」と言い切ってよいものかは私には分かりません．

ｗ さんのレス (2005/08/27(Sat) 00:09)

篠原さんほんとありがとうございます．自分は回路の場所場所で電界に強弱をできるなんて考えもしてなかったので，だいぶ助かりました．もし強弱ができてないとおかしい点がたくさんでてくるので，帯電でなくとも何らかの方法で強弱をつけてると自分は理解したいと思います．つまり抵抗には電界を強く，抵抗が小さいところは弱く，抵抗がないところには，電界はつくらない・・・・・・あれ？ それだと自由電子が動かなくなる．やばっ，また疑問が・・・

篠原 さんのレス (2005/08/27(Sat) 00:23)

抵抗がない物質，つまり超伝導体については，私も分かりません． 電界が存在しないことは確かですが，なぜ電界がないのに電荷が動くんでしょうね．私も疑問に思います．

これ以上のことについては，説明できる方は少ないんじゃないでしょうか． また，説明されても理解できないような気がします．

どうしても，気になるのであれば，大学へ行き，ご自分で勉強してください． 通常の超伝導体においては，BCS理論というもので，説明できるそうです． また，高温超電導体については，まだ分からない点が多いようです．

勉強がんばってください．

渡邉　矩章 さんのレス (2005/08/27(Sat) 00:40)

>等速運動みたいな状態になるんじゃないでしょうか？

そのように想像するのが，高校の範囲で考えれば必然的な結論だと思います． ただ個人的な意見として「電子」を電気回路の話で出すのはお勧めできません． この掲示板でも話をややこしくしたのは大体，導線の抵抗や電子などだと思っています．

このときこの回路を最も特徴付けるもの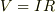は あるいは 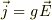という法則に従っているという事，それに尽きると思いますよ． ただしこの法則の基礎は，電磁気学の外にあります．電子などが関わってくる のはここのあたりではないでしょうか．

FKD さんのレス (2005/08/27(Sat) 00:43)

>渡邉さん 書いたあとに自信がなくなって削除してしまいました．すいません．． 話のつながりがわからなくなるので再掲載します．

***

>電界が存在しないことは確かですが，なぜ電界がないのに電荷が動くんでしょうね．

電界がないからといって必ずしも電荷が動かないことにはならないと思います． まったく力を受けていない粒子は慣性の法則に従って等速運動or静止しますよね． 単なる憶測なのですが， 等速運動みたいな状態になるんじゃないでしょうか？ （もちろん，経路は曲がっているのでこれは比喩表現ですが）

篠原 さんのレス (2005/08/27(Sat) 00:50)

渡邉矩章さんへ

たしかに，「電子」や「導線の抵抗」を持ち出すと，話はややこしくなります． しかし，質問の内容に「電界」などが出てきたこと，「導線中をなぜ電荷が移動できるか」などを含んでいたことなどを考え，話を掘り下げて説明しました．

掲示板を荒らすような状態になったこと，お詫びいたします． もっと，分かりやすい説明が出来るよう，勉強いたします．

ｗ さんのレス (2005/08/27(Sat) 01:11)

みなさん，本当にありがとうございます． 自分は独学で物理を勉強しはじめ，電磁気学で行き詰まり，いろんな参考書，専門書（少し）をもってしてもわからなかった問題をこの掲示板で見事に解決することができました．回路内に電荷がたまり電源が作り出す電界を打ち消すという誤解をしていたことと，電池が電界を振り分けられるということを知らなかったことが今回自分が悩んだ原因でした．電源がどうして電界を振り分けれるか，超伝導体についてはまだまだ疑問が残りますが，そこはなるものはなるというように理解して機会があれば調べて生きたい思います．皆さん本当にご指導ありがとうございました．

渡邉　矩章 さんのレス (2005/08/27(Sat) 01:30)

＞等速運動みたいな状態になるんじゃないでしょうか？ （もちろん，経路は曲がっているのでこれは比喩表現ですが）

なるほど，回路だから曲がるんですね（言い訳としては電源，抵抗を直線の 導線で結べば，等速直線運動になる状態はつくれる）． 「電磁気学１太田浩一著」によれば，オームの法則を守るように 電荷が導体表面に誘導されるそうです．だから円の回路の場合なら， 電荷の分布などが計算できそうな気がします．

＞＞篠原さんへ 篠原さんの主張は分かります．僕が上に書いた文章はただの個人的な趣味の問題です．書く必要ありませんね．以後気をつけます．