無題
無題
7star さんの書込 (2005/08/16(Tue) 04:36)
はじめまして.私は東京大学の理科?類の1年生です.9月に期末試験があるので力学を勉強しているのですが,物理はすごく苦手で全然わかりません・・・.今過去問を解いていたのですが,どうもうまくいかないので教えていただけると助かります.間違いがあれば指摘していただけないでしょうか?
質量  の質点が自然長
の質点が自然長 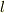 ,ばね定数
,ばね定数  のばねで静止している点Oにつながれ,この点Oのまわりに角速度ωで回転している.但し,
のばねで静止している点Oにつながれ,この点Oのまわりに角速度ωで回転している.但し, 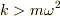 である.ばねは直線状で,動径方向にしか運動しないものとする.
?ばねが振動していないときのばねのののびはいくらか.
?ばねが振動しているときの振動数はいくらか.
?
である.ばねは直線状で,動径方向にしか運動しないものとする.
?ばねが振動していないときのばねのののびはいくらか.
?ばねが振動しているときの振動数はいくらか.
? 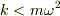 のとき,質点はどのような運動をするか.
のとき,質点はどのような運動をするか.
というものです.?と?はなんとか自力で解けました.
?は 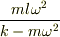 ?は
?は 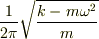 となりました.
となりました.
?についてなんですが,ばねの長さrについての微分方程式を立てると
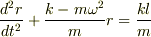
となって, 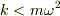 なので,この微分方程式の斉次の解を求めようとすると
なので,この微分方程式の斉次の解を求めようとすると
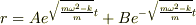
特殊解は,加速度0とおいて(つまりこの解は振動の中心を表す)
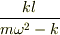
となりました. ということはこの微分方程式の一般解は
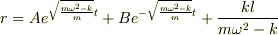
ということになると思うのですが,これが一体質点のどのような運動を 表しているのかがさっぱりです・・・.単振動なんでしょうか? どうかご教授願います.
Re: 無題
yama さんのレス (2005/08/16(Tue) 12:14)
?ですが,計算をしなくても,大体どのような運動になるかはちょっと考えれば分かります. この場合の力は,Oから遠ざかる向きにはたらき,点Oからの距離とともに単調に増加するので,点Oに向かって引き戻すような復元力ははたらきません. 従って質点は振動することはなく,Oからいくらでも遠ざかり続け,ばねはいくらでも伸び続けます. ただし,実際にはばねが伸びきってしまうか,ばねが切れてしまうでしょう.
ただ単に,方程式を解いたらこうなったというのではなく,物理的な考察が大切です.
回転するばね
山旅人 さんのレス (2005/08/16(Tue) 14:23)
質点の運動を記述する微分方程式を作ってみましょう.運動を極座標で表すと,
運動エネルギーK=(1/2)m<b>v</b> 2 =(1/2)m((dr/dt) 2 +(rdθ/dt) 2 ) … (1) 位置エネルギーU=(1/2)k(r−l) 2 … (2) ラグランジアンL=K−U
運動方程式(r成分) (d/dt)(∂L/∂v)−∂L/∂r=0より
md 2 r/dt 2 +mr(dθ/dt) 2 −k(r−l)=0 … (3)
(θ成分) (d/dt)(∂L/∂(dθ/dt))−∂L/∂θ=0より
2mr(dr/dt)(dθ/dt)+mr 2 (d 2 θ/dt 2 )=0 … (4)
質点は,連立微分方程式(3)(4)で支配される運動をします.7star さんがお書きの<微分方程式>は,(3)で dθ/dt=ω(一定)の解を求めようとするものですが,これを(4)に代入するとmr(dr/dt)=0,すなわち<b>r=一定</b> となります.これが?です.
すなわち,ばねが振動するときは,回転の角速度 ω は一定にはなりません. それでは,(3)(4)がどのような解をもつのか,これからゆっくり調べてみましょう.
>> yama さん 「物理的な考察」 をすれば, > 質点は振動することはなく,Oからいくらでも遠ざかり続け,ばねはいくらでも伸び続けます. > ただし,実際にはばねが伸びきってしまうか,ばねが切れてしまう…
ようなことが現実には起こりえないことは明々白々では!?!
Re: 回転するばね
FKD さんのレス (2005/08/16(Tue) 15:14)
?なんですが, 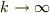 あるいは
あるいは 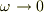 で
で 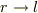 にならないとまずいのでは?
にならないとまずいのでは?
Re: 回転するばね
yama さんのレス (2005/08/16(Tue) 16:04)
問題文を読むとωは与えられた定数のように思われます. たとえば,ばねが細長い筒の中に入っていて,筒全体が外力によって一定の角速度ωで回転しているような状況です. そうでないと,「動径方向にしか運動しない」という条件が無意味になってしまいます. また,ωが変化したのでは k<mω 2 という条件も意味がなくなります. 問題文に多少曖昧なところはありますが,問題全体を総合的に読むとωは定数と考えるのが妥当だと思います.
FKDさんへ ?で求めたのはばねの長さではなく,ばねののびです. ばねののびは k→∞のときも,ω→0 のときも0になります.
Re: 回転するばね
FKD さんのレス (2005/08/16(Tue) 16:14)
>>yamaさん 勘違いしてました.すいません.
Re: 回転するばね
山旅人 さんのレス (2005/08/16(Tue) 16:14)
ひとつ上のレスの続きです. 連立微分方程式(3)(4)は,例えば
- r=r 0 sinωt+l … (5)
- θ=θ 0 cosΩt… (6)
のような単純な振動解はもたないようですね.カオスのようなことが起こりそう(?).牛刀(無限級数解)を持ち出します? やりたくない.
一端を固定し,他端に質量mのおもりをつけたばねをなめらかな水平面にねかしておき,おもりにばね方向と直角方向に v 0 なる初速度を与えたときに以後のおもりの運動を問う,という問題にもなっているのですが,難しいようです.
> ?なんですが,k→∞ あるいは ω→0 で r→l にならないとまずいのでは?
?は “のび” なので,k→∞ あるいは ω→0 で のび→0 となるので問題はないようです.
Re: 回転するばね
ラジオ さんのレス (2005/08/16(Tue) 17:44)
お邪魔します. 問題に「k>mω^2」とありますので,指数関数の√の中は負になりますね. そうするとこれは exp(iΩt) という形になりますので,振動です. 解の第3項は定数ですので,これが振幅の中央の長さ,その前後で 振動するわけです.AとBは初期条件から決まる定数です.
このままでよく解けていると思いますよ.
Re: 回転するばね
yama さんのレス (2005/08/16(Tue) 18:16)
?は k<mω^2 の場合なのですが・・・ √の中が正になるので,有界な運動にはなりません.
Re: 回転するばね
yama さんのレス (2005/08/16(Tue) 21:12)
山旅人さんへ
あなたが導かれた方程式は,題意には合っていないように思いますが,それはともかくとして積分することはできます. まず(4)を積分すると r 2 (dθ/dt)=M となります.積分定数Mは角運動量です. これから dθ/dt=M/r 2 になるので,これを(3)に代入するとrだけの方程式になり,エネルギーの積分を利用すると,tをrの楕円積分で表すことができそうです. 従って,rはtの楕円関数で表せると思います. rは周期的ですが,M>0のときはdθ/dtが常に正なのでθは単調増加になります.
Re: 回転するばね
ラジオ さんのレス (2005/08/16(Tue) 21:13)
> ?は k<mω^2 の場合なのですが・・・ > √の中が正になるので,有界な運動にはなりません.
おっしゃるとおり,私の間違いです.問題を見誤っていました. ハズカシイ・・・ たしかに,これは「ばねが弱すぎて振動にならない. 遠心力でばねが伸びると,さらに遠心力が強まり, その結果さらにばねが伸びる」ということで どんどんばねが伸びてしまう条件になっていますね. 失礼しました.
Re: 回転するばね
ラジオ さんのレス (2005/08/16(Tue) 21:36)
あっ,そんなに簡単ではないかも. 解の式を見ると,未定係数Aが0なら伸びの長さは一定値(振動の中心)へ 収束するようですね.初期条件を適当に選ぶとAは0にできますから, そういう運動もありえそうです.
例えば初期の長さをR0,速度をv0とし, 振動中心の長さをr0,√の部分をδとすると, R0-r0-v0/δ=0の場合にはA=0となるようです. この場合は,最初ちょっと長めにしておいて,中心方向へ初速度を 与えてやることになるわけですね.そうすると一種の減衰運動となって, 一定値へ収束する,というわけですね. うーん,本当にこんな運動がおきるのだろうか?? あるいはもっと一般的な条件があるのだろうか???
(文中に式を書けなくてゴメンナサイ)
Re: 回転するばね
ラジオ さんのレス (2005/08/16(Tue) 21:48)
何度もすみません.訂正します.
誤R0-r0-v0/δ=0の場合にはA=0となるようです. 正R0-r0+v0/δ=0の場合にはA=0となるようです.
ひさびさにこんな問題を解いて楽しくなったものですから….
Re: 回転するばね
ラジオ さんのレス (2005/08/16(Tue) 22:10)
あっっ! まだありますね.A<0の場合です.これも初期条件次第で作れますね. この場合,式の上ではrは負になって発散しますね. 実際にはそこまで行くことはありえませんからr=0になった時点で この式の適用限界,ですね. 「運動量が保存しないじゃないか!」と思われるかもしれません. これはω=一定,という条件によって,運動量が保存しない系のことを 扱っているのだと考えれば納得行きます.
じゃあ,どういう場合に,なぜr=0にまでばねは縮んでしまうのか? これは初速度が負の場合ですね(厳密にはもっと条件が必要なんでしょう). 初速度が負でばねが縮むと遠心力が弱まる,そうしてもっとばねは縮む, の繰り返しです.ばねの反発力には縮む方向の運動量が勝ってしまう, ですね,きっと.
そうやって考えると, ・A=B=0というのが最初から長さが変化しない一定の回転状態 ・ただしこれは不安定平衡解というやつなので −外力があるとどんどん伸びたり −どんどん縮んだりしてしまう, ということなのでしょうか. しかも(上記のように)うまく条件を選ぶと, ・平衡状態へ収束する解もある
うーむ,これは奥が深い問題ですね.
Re: 回転するばね
山旅人 さんのレス (2005/08/16(Tue) 22:53)
>> yama さん > あなたが導かれた方程式は … 積分することはできます. > これから dθ/dt=M/r 2 になるので … エネルギーの積分を利用すると … rはtの楕円関数で表せる ….
ご教示ありがとうございます.確認致しました. 昔ひととおりやったことをすっかり忘れておりました.歳はとりたくないものです.
> rは周期的ですが,dθ/dtが常に正なのでθは単調増加になります.
dθ/dt=M/(mr 2 ) (M:角運動量),rが周期的なので,dθ/dt は周期的となります.『回転』 なので 「θ は単調増加」 は当然でしょうか.
> 題意には合っていないように思いますが…
ここは,見解の相違としか申しあげようがありません. <b>定数 ω</b> が mω 2 >k のとき確かに <b>どんどんばねが伸びてしまい</b> ますが,これを実現するためには質点が得る 「どんどん大きくなるエネルギー」 を ω を一定に保つための外力が供給しなければなりません. 「こんなことを考察して,いったい何の益があるのか.それより <b>振動するrと ω</b> の関係を考察する方が生産的」 が私の見解です.
しかしながら,学部1年生の力学の問題となると,ω は一定と考えることが穏当か,と思ったりもします.
Re: 回転するばね
yama さんのレス (2005/08/16(Tue) 23:00)
7starさんの計算は一部間違っているように思います. 加速度0としたときは r=kl/(k-mω^2) になります. しかし,このrは負になってしまいます. r>0でなければならないので,加速度が0にはならないということです. このことは力がどこでも0にはならないことからも分かります. つまり,振動の中心になるような平衡点は存在しません. 平衡点自体が存在しないので,平衡点に収束する解はありません. なお,r=0 は特異点なので,除外して考えないといけません.
山旅人さんへ
角運動量のところでmが抜けていたようですね.訂正ありがとうございます.
Re: 回転するばね
ラジオ さんのレス (2005/08/17(Wed) 01:25)
> このことは力がどこでも0にはならないことからも分かります.
なるほど・・・ばねの力と遠心力を比較してみれば一目瞭然ですね. ということは,やはりどんどん伸びていく解だけですね. 勉強になりました.難しい数式を使うより,よく考えてみれば 当たり前のことなんですね.勉強になりました.
(収束するような面白い解が出なかったのがちょっと残念)
Re: 回転するばね
yama さんのレス (2005/08/17(Wed) 09:18)
初期条件によっては一旦Oに近づいた後,向きを変えてOから遠ざかる運動も可能です. また,有限時間でOに到達するような運動もありそうに思えますが,Oに達した後はどうなるのかという問題が生じますし,そもそもばねの長さが0になるのか疑問ですから,このような解はやはり除外すべきでしょうね.
Re: 回転するばね
7star さんのレス (2005/08/17(Wed) 14:11)
皆さん本当にありがとうございます. どうやら結構難しい問題みたいですね・・・.
>加速度0としたときは r=kl/(k-mω^2) になります. しかし,このrは負になってしまいます. r>0でなければならないので,加速度が0にはならないということです.
とありますが,一応私の答えではr=kl/(mω^2-k)になってるんですがこれでは違うんですかね?一応負にならないようにしたんですが・・・. 皆さんのレスを読んでいると,結論は「どんどん伸び続ける」ってことでいいんでしょうか?運動方程式を立てるとどうしても振動にはならない気がしましたが.
もう少し皆さんのお知恵を拝借したいです.参考までに,うちのクラスメートが解いてくれたのをアップしておきます.彼は単振動だと言ってますね・・.しかも運動方程式はばねの伸びについて立ててますので私のとは違いますが・・・.
Re: 回転するばね
yama さんのレス (2005/08/17(Wed) 16:12)
r=kl/(mω^2-k) をもとの方程式に代入しても加速度は0になりません. また,rがどんな正の値をとっても加速度は0になりません. すなわち,加速度は決して0にならないということです. 加速度が0になるような特殊解は存在しないとも言えます. あなたが求めた一般解は,その点で修正が必要です.
クラスメートの解は,形式的には三角関数で表されていますが,引数が虚数なので,実数になるように書き直すと結局は指数関数で表されることになります. 従って,単振動ではありません. 初期条件によっては一時的に縮むことはありますが,最終的にはのび続けることになります.