テンソルの演算について

スウさんの書込 (2005/08/02(Tue) 20:23)

はじめまして．『スウ』と申します．私は大学院生で専攻は物理学です．

前期に一般相対性理論の講義を受けたのですが，テンソルがいまいちよくわかりません．そこでテンソルの加法，乗法，縮約，微分を証明してみようと思い自分なりに加法，乗法についてはやってみたのですがあっている自信が無いので，どなたか添削していただきたいと思っています．また，縮約，微分についてはよくわからなくなってしまったので教えていただければ幸いです．よろしくお願い致します．

加法

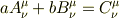
$aA^{\mu}_{\nu} + bB^{\mu}_{\nu} = C^{\mu}_{\nu}$

証明

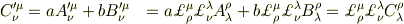
$C^{\prime \mu}_{\nu} &= aA^{\prime \mu}_{\nu} + bB^{\prime \mu}_{\nu}&= a\pounds^{\mu}_{\rho}\pounds_{\nu}^{\lambda}A^{\rho}_{\lambda} + b\pounds^{\mu}_{\rho}\pounds_{\nu}^{\lambda}B^{\rho}_{\lambda}&= \pounds^{\mu}_{\rho}\pounds_{\nu}^{\lambda}C^{\rho}_{\lambda}$

乗法

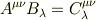
$A^{\mu \nu}B_{\lambda} = C^{\mu \nu}_{\lambda}$

証明

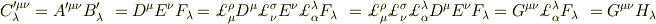
$C^{\prime \mu \nu}_{\lambda} &= A^{\prime \mu \nu}B^{\prime}_{\lambda}&= D^{\mu}E^{\nu}F_{\lambda}&= \pounds^{\rho}_{\mu}D^{\mu}\pounds^{\sigma}_{\nu}E^{\nu}\pounds_{\alpha}^{\lambda}F_{\lambda}&= \pounds^{\rho}_{\mu}\pounds^{\sigma}_{\nu}\pounds_{\alpha}^{\lambda}D^{\mu}E^{\nu}F_{\lambda}&= G^{\mu \nu}\pounds_{\alpha}^{\lambda}F_{\lambda}&= G^{\mu \nu}H_{\lambda}$

縮約

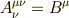
$A^{\mu \nu}_{\nu} = B^{\mu}$

微分

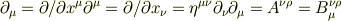
$\partial _{\mu} = \partial / \partial x^{\mu}\partial ^{\mu} = \partial / \partial x_{\nu} = \eta^{\mu \nu}\partial _{\nu}\partial _{\mu} = A^{\nu \rho} = B_{\mu}^{\nu \rho}$

Re: テンソルの演算について

yama さんのレス (2005/08/03(Wed) 23:25)

何を証明したいのかよく分かりませんが，演算の結果がテンソルになることを証明したいのでしょうか？加法，乗法，縮約の結果がテンソルになることは，変換の式を書くまでもなく，ほとんど自明だと思いますが・・・微分については，あなたが書かれた式は添字の整合性がとれておらず，意味がありません．そもそも，テンソルを座標で微分しても，一般にはテンソルにはなりません．（スカラーを微分した場合はベクトルになりますが）テンソルになるようにするには，共変微分を考える必要があります．

Re: テンソルの演算について

スウさんのレス (2005/08/04(Thu) 21:08)

>何を証明したいのかよく分かりませんが左辺＝右辺となることを証明したかったんです．

>微分については，あなたが書かれた式は添字の整合性がとれておらず，意味がありません．大変失礼いたしました．

Re: テンソルの演算について

yama さんのレス (2005/08/04(Thu) 21:26)

>左辺＝右辺 >となることを証明したかったんです

あなたの書かれた式は恒等式ではないので，何の前提もなしに証明することはできません．

[home] [掲示板] [ページの先頭]