運動方程式

うさぎさんの書込 (2005/07/25(Mon) 14:45)

こんにちは♪私は今大学で物理を勉強しています(^＿^) 高校でも２，３年のときに物理を習っていましたが，とても苦手です…．つい最近，学校の前期のテストがあり，そのテスト勉強時に２次元極座標表示で運動方程式を書き下すところまでは教科書を読んでいくとなんとか理解できたのですが，３次元の場合が分かりません．そこで，

「３次元極座標表示の運動方程式を書き下せ．」

という問題に対してどのように答えればいいのか教えてください（o＞＿＜o）どうぞよろしくお願いします☆

Re: 運動方程式

渡邉　矩章さんのレス (2005/07/25(Mon) 16:35)

はじめまして．2次元の場合を書いてもらって，どうして3次元だと分からないかを説明してもらえるとレスがつきやすいのかもしれませんね．

Re: 運動方程式

うさぎさんのレス (2005/07/25(Mon) 16:53)

２次元の場合 x=rcosθ，y=rsinθ と極座標で表せる． x"=(r"-rθ'^2)cosθ-(rθ"+2r'θ")sinθ y"=(r"-rθ'^2)sinθ+(rθ"+2r'θ')cosθ Newtonの運動方程式に代入して整理すると m(r"-rθ'^2)=Fr m(rθ"+2r'θ')=Fθ

3次元の場合，まずどのように極座標で表せばよいのか分かりません．そして，その後は２次元と同じように２回微分してNewtonの運動方程式に代入していけばよいのかなぁと思いますが，最後の整理の仕方も分かりません．

Re: 運動方程式

渡邉　矩章さんのレス (2005/07/25(Mon) 17:59)

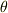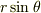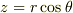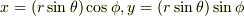2次元を3次元の場合の断面として考えれませんか？ x-y平面への射影は，質点とｚ軸を通る平面で考えると質点の位置とｚ軸とのなす角を $\theta$ とすれば， $r \sin\theta$ です（つまりｚ軸への射影は $z=r\cos\theta$ ）．今度はｘ軸とその射影のなす角を $\phi$ とすると2次元の場合と同じように $x=(r\sin\theta )\cos\phi , y=(r\sin\theta )\sin\phi$ ．

ところで参考書は持っていないのですか？

Re: 運動方程式

うさぎさんのレス (2005/07/25(Mon) 19:25)

教科書は持っていますが，参考書は持っていません…．教科書では３次元の場合は省略されています（＞＿＜;）

x,y,zをそのようにおいた後，何で微分したら良いのでしょうか?? 極座標は距離と角度で表されているので，とても頭の中がこんがらがってしまいます．どうぞ教えてください☆

Re: 運動方程式

渡邉　矩章さんのレス (2005/07/26(Tue) 00:04)

どうぞご自分でお考えください★

Re: 運動方程式

ｙama さんのレス (2005/07/26(Tue) 14:06)

No.6249で渡邉氏が書かれている式を用いて，2次元の場合と同様に計算すればいいだけです．つまり，座標（x,y,z）を時間で2階微分して加速度aを求めます．運動方程式は ma=F ですが，これをr方向，θ方向，φ方向の成分に分けて表さないといけません．そのためには，それぞれの方向の単位ベクトルと上の式の内積をとります．たとえば，e _r との内積をとると，右辺は F・e _r になりますが，これはr方向の力の成分 Fr なので，ｒ方向の運動方程式は結局 ma・e _r =Fr となります． θ方向，φ方向についても同様です．なお，単位ベクトルの成分を求める方法はいろいろありますが，たとえば単位ベクトルが座標軸となす角を考えて図形的に求めることができます．

なお，余計なことかもしれませんが，教科書で分からないところや，発展的な内容を調べるために，参考書を持っていたほうがいいと思います．

Re: 運動方程式

うさぎさんのレス (2005/07/26(Tue) 14:36)

分かりました!! ありがとうございました☆

[home] [掲示板] [ページの先頭]