るい さんの書込 (2005/07/24(Sun) 19:29)

お久しぶりです．

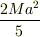えっと，剛体の問題で， 半径aの剛体球の中心の慣性モーメントは なのに， 同じ剛体球を長さlの糸につるし振り子としたときの剛体球の中心の慣性モーメントは 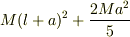となるのはどうしてですか？ 剛体球振り子のときも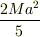， だと思ったのですが…．

yama さんのレス (2005/07/24(Sun) 23:23)

この場合は，振り子の支点のまわりの，振り子全体の慣性モーメントのことだと思います．

るい さんのレス (2005/07/25(Mon) 00:01)

yamaさん，答えてくださってありがとうございます． えっと，それでは，糸の長さｌ，剛体球の半径a，質量Mの振り子の運動を考えるとき，糸が鉛直となす角をθ，剛体球の角をφとおき，鉛直下向きの軸をｘとし水平をｙ軸とします． それで，球の中心の座標を 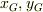とかくと， 球の中心の慣性モーメントを 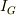とおいているなら， 運動系のラグランジアンを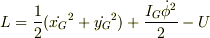， と表すのは正しいということですか？

Joh@Kyoto さんのレス (2005/07/25(Mon) 01:08)

回転モーメントは，どこを回転の中心軸とするかで，同じ物体でも値が変わってきます．回転モーメントの物理的意味は「物体の回しにくさ」でしたから，当たり前ですね．回転軸が重心とずれている場合には，「平行移動の定理」とか，そのような名前の定理があると思いますよ．

ｙama さんのレス (2005/07/25(Mon) 10:27)

Mが抜けているのを直せば，そのラグランジアンは正しいと思います． もちろん，xとyは独立でないとので，θで表したほうがいいでしょうし，φ=θ と置けると思います.

るい さんのレス (2005/07/25(Mon) 21:30)

分かりました！ yamaさん，Joh@Kyotoさん，ありがとうございました．