不確定性原理と無限井戸

不確定性原理と無限井戸

まきお さんの書込 (2005/07/24(Sun) 17:53)

はじめまして，いま大学四年のまきおと申します． 実は，大学院の口述試験を一週間後に控えて，量子力学に関する 疑問ができてしまいました．是非，ご教授ください．

質問内容なのですが，これは，無限の井戸型ポテンシャル中の波動関数を 求めているときに，ふと引っかかってしまいました．

幅Lの井戸型ポテンシャル内の一つ一つの固有関数

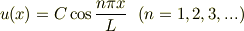
u(x)=C\cos\frac{n\pi x}{L}\ \ (n=1,2,3,...)

に対して固有値（固有エネルギー？）は

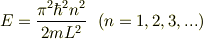
E=\frac{\pi^2 \hbar^2 n^2}{2 m L^2}\ \ (n=1,2,3,...)

となります． ここで，疑問に思ったのが，もし粒子の波動関数が， 上の固有関数の中の一つだけと一致していたら，やはり，１００％ その固有値を観測することができるはずだと思いました． 次に，（実はここが間違いかもしれないのですが，） エネルギーEは運動量pを使ってあらわすと

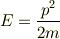
E=\frac{p^2}{2m}

であるので，運動量が不確定性が無く観測ができるのではないかと 思いました．幅がLの井戸なので，位置の不確定性は有限です． すると，あれ？不確定性原理の式にあわないではないですか．． いったいこれはどういうことなのでしょうか？

もし，エネルギーと運動量の等式が成り立っていないとしたら， では，運動エネルギー以外に，何のエネルギーがあるのでしょうか？

よろしくお願いします．

Re: 不確定性原理と無限井戸

渡邉　矩章 さんのレス (2005/07/24(Sun) 18:04)

はじめまして．僕も昨日，口頭試問を受けてきました．

＞もし粒子の波動関数が， 上の固有関数の中の一つだけと一致していたら，やはり，１００％ その固有値を観測することができるはずだと思いました．

これは，あくまで「もし」ですよね．理想観測の場合に定常状態ならば，２回目以降は1つの固有関数になりますので，100パーセント1回目と同じ固有値を観測しますよ．たしか観測がフィルターのような役割をするイメージだと参考書に書いてありました．

ただフィルターを通したとしても縮退がある場合は，１つの固有関数にはなりません．たとえば水素原子のエネルギー固有値に対してフィルターをかけても，まだ色々な状態がありますよね．

だからその考えで正しいと思いますよ．ただ，一般の状態は固有関数の線形結合だと思いますので，観測前にどの固有値を得るかは確率的にしか知りえないと思います．

最後に批判的な目で見るようにお願いしたいと思います．メシア１にある程度詳しいことが書いてあると思いますのでそれを読むと安心できるかもしれません．

Re: 不確定性原理と無限井戸

まきお さんのレス (2005/07/24(Sun) 19:01)

渡邉さん＞ すばやい返信ありがとうございます！！！ いいですねっ，いち早く夏が来たのですね〜．

＞これは，あくまで「もし」ですよね． なるほど，ということは，不確定性原理というのは， 一般の波動関数が，観測前は必ず固有関数の線形結合であるということ を述べているのでしょうか．

また，観測されたエネルギーEから運動量pを求めることができる，つまり 私が書いた

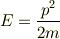
E=\frac{p^2}{2m}

がオッケーだとすると，測定したエネルギーから，運動量を求めることが できてしまい，運動量の固有方程式は必要ないと思っちゃいます^^

Re: 不確定性原理と無限井戸

渡邉　矩章 さんのレス (2005/07/24(Sun) 19:26)

＞一般の波動関数が，観測前は必ず固有関数の線形結合であるということ を述べているのでしょうか．

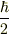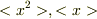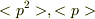不確定性原理とはあまり関係ないと思います．あと線形結合は１つの固有関数の場合を含むつもりで書きました．それと不確定性原理はΔｘとΔｐの積がいつでも \frac{\hbar}{2} より小さくはなりません．これは交換関係が直接関係しています．直接的な値は <x^{2}> , <x> と <p^{2}> , <p> を計算すればもとまると思いますよ．

Re: 不確定性原理と無限井戸

yama さんのレス (2005/07/24(Sun) 20:52)

この場合の固有関数は実数値の三角関数だから，運動量の固有関数ではありません．運動量の固有関数は複素数値の指数関数だからです． 従って運動量は確定値をとりません． なお，井戸の中だけを考えれば，運動量 p と -p の固有関数の重ね合わせのように見えます．だとすると，運動量は p と -p のどちらかの値をとるのかというと，そうでもありません． 運動量の固有関数は無限に広がっているので，この２つを重ねても井戸の外では 0 にならないからです．井戸の外で 0 にするには無限個の異なる運動量の固有関数をフーリエ積分の形で重ね合わせる必要があります．

Re: 不確定性原理と無限井戸

まきお さんのレス (2005/07/24(Sun) 21:22)

渡邉さん＞ n番目の固有関数

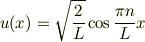
u(x)=\sqrt{\frac{2}{L}}\cos\frac{\pi n}{L}x

において，?P(<p^2>-<p>^2)を求めてみました．すると，

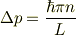
\Delta p = \frac{\hbar \pi n}{L}

となり，運動量は不確定性がありました（^ー^ しかもこれを二乗して，2mで割ると，そのとき観測されるエネルギーと等しい みたいです．ポテンシャルが０で，運動量の平均値が０であるから，エネルギーの 平均は０，しかし，運動量の分散?pはある有限の値を持つので， それを二乗した数を2mで割ったものが観測されるエネルギー，なのでしょうか． いい加減な考察ですいません．

yamaさん> 返信ありがとうございます．確かに，固有関数にはならないですね＾＾ おかげさまでその部分をはっきりできました！ ※呼び捨てにしてしまいました．もうしわけないですm(__)m

Re: 不確定性原理と無限井戸

yama さんのレス (2005/07/24(Sun) 22:23)

>ポテンシャルが０で，運動量の平均値が０であるから，エネルギーの平均は０

運動量は正と負の値をとるので平均では０になりますが，運動エネルギーは負にはなりません． 従って，エネルギーの平均値も０にはなりません．

Re: 不確定性原理と無限井戸

渡邉　矩章 さんのレス (2005/07/24(Sun) 22:54)

>?P(<p^2>-<p>^2)を求めてみました．すると，

となり，運動量は不確定性がありました（^ー^ しかもこれを二乗して，2mで割ると，そのとき観測されるエネルギーと等しい みたいです．

これは<p>=0ならばΔｐ=√(<p^{2}>) なので

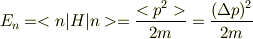
E_{n}=<n|H|n>=\frac{<p^{2}>}{2m}=\frac{(\Delta p)^{2}}{2m}

で何も不思議なことは無いと思いますよ．ただ，ここのところをあまり考えたことは無いので自信はありません．

Re: 不確定性原理と無限井戸

まきお さんのレス (2005/07/24(Sun) 23:31)

みなさま，本当にありがとうございます！ まず，質問内容を少しまとめます．

１.井戸型ポテンシャル中の固有関数の1つを波動関数にもつ粒子のエネルギーを 観測したとき，そのエネルギーから下の式にしたがって運動量を求められてしまうの ではないか．

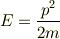
E=\frac{p^2}{2m}

そして，それは不確定性原理に反するのではないか．

２.そのとき観測される運動量のあいまいさと，その波動関数の確定したエネルギーの 値は等しいのはなぜか．

１．yamaさんに教えていただきまして，なんとなくわかりました． まず，井戸型ポテンシャルの固有関数の表記，

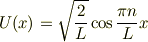
U(x)=\sqrt{\frac{2}{L}}\cos\frac{\pi n}{L}x

というのが，井戸型ポテンシャルの外を含めた関数を表していないことに注意 しなければなりませんでした．実際は，井戸の中だけがポッコリしてる関数です． 1つの固有関数を波動関数にもつ粒子の場合，エネルギーは確定した値をとることが できます． しかし，得られたエネルギーから，運動量を求めることはできません． なぜなら，上のu(x)は，無限遠まで続く周期関数であるからです．もし波動関数が この形（無限遠まで続く波）であるならば，確定した運動量を求めることが出来ますが，実際は，井戸の中のみが膨らんでる波動関数です． このような波は，さまざまな振動数・振幅のcos波からなっているので，つまりは沢山の運動量からなっているわけです．よって，運動量はある程度の不確定性をもちます．

２，こちらは渡邉さんに教えていただきました． 私の力不足で，いまだに関数での表記しかできませんので，これでよろしいでしょうか．

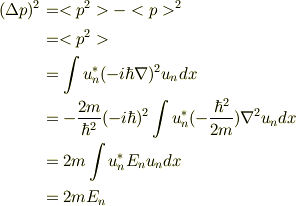
(\Delta p)^2 &=<p^2>-<p>^2\\&=<p^2>\\&=\int u_n^*(-i\hbar\nabla)^2 u_n dx\\&=-\frac{2m}{\hbar^2}(-i\hbar)^2 \int u_n^*(-\frac{\hbar^2}{2m})\nabla^2 u_n dx\\&=2m\int u_n^* E_n u_n dx\\&=2m E_n

対象としている粒子の運動量や，位置のあいまいさは，その波動関数の形に関係しているのですね．エネルギーの固有関数と，運動量の固有関数を別々にかんがえていました．

えらそうにつらつらと書いてしまいましたが，これで大丈夫・・・ですよねっ！＾＾；

Re: 不確定性原理と無限井戸

ｙama さんのレス (2005/07/25(Mon) 12:13)

>もし波動関数がこの形（無限遠まで続く波）であるならば，確定した運動量を求めることが出来ますが

この場合でも運動量は確定値はとりません． 2cos(kx)=exp(ikx)＋exp(-ikx) なので，U(x)は運動量pと-pの2つの固有関数の重ねあわせになります． 従って運動量を測定すると，同じ確率でpまたは-pが得られます． もちろん運動量の絶対値pは確定値をとりますから E=p 2 /2m は成り立ちます. 一般に，E=p 2 /2m が成り立つのはEとp（の絶対値）が確定値をとる場合です． pが確定値をとらない場合は E=<p 2 >/2m が成り立ちます．

Re: 不確定性原理と無限井戸

まきお さんのレス (2005/07/25(Mon) 14:17)

>yamaさん なるほど！たしかにそうですね＾＾ それは，Ｅからpを求めるときにプラスとマイナスの二つの解が あることに対応しているのですね！なんだか，量子力学は根が深いです＾＾

井戸方ポテンシャルを解くと，エネルギーは確定しても，運動量は確定しない という性質が見れましたが，これは，運動量を観測した結果が

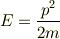
E=\frac{p^2}{2m}

が成り立たないことがある，ということなのでしょうか？エネルギーは人間が 定義した量ですよね．すると，量子力学など関係なしに，この等式は成り立つと 思うのですが・・・． なんだか，次から次へと，申し訳ないです．よろしくお願いします．

Re: 不確定性原理と無限井戸

渡邉　矩章 さんのレス (2005/07/25(Mon) 15:16)

質問の内容に直接は関係ないのですが（上の質問のヒントになるかもしれません） 書き方で少し気になるところがあります． 正直なところ

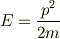
E = \frac{p^{2}}{2m}

は見たことが無いと思います．左辺が固有値（右辺が演算子）なのかと思ってしまいます． よく目にするのは

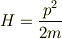
H= \frac{p^{2}}{2m}

という書き方です（この式は固有値でなく演算子です）．

Re: 不確定性原理と無限井戸

ｙama さんのレス (2005/07/25(Mon) 17:15)

そうですね．渡邉氏の書かれている通り，演算子の間の関係なので，観測値の間に常に同じ関係が成り立つとは言えないでしょう．

Re: 不確定性原理と無限井戸

まきお さんのレス (2005/07/25(Mon) 17:36)

渡邉さん，yamaさん，ご返答ありがとうございます． えっと，私はどうやら，古典的な思考から脱することができないようです（汗

私は，運動量とエネルギーの等式を古典力学のつもりで書いていました． 渡邉さんのご指摘で，演算子同士の等式が成り立つことは確認できました． しかし，私が気になるのは，観測したエネルギーと運動量に古典力学的な 関係がいつも成立するとは限らない，というところです． もし観測した運動量が，確定したエネルギー値から，古典的に見積もった値より 大きい場合，その差のエネルギーはどこからきたのでしょうか？

エネルギー保存則は，量子力学の世界では成り立たないということでしょうか・．

Re: 不確定性原理と無限井戸

ｙama さんのレス (2005/07/26(Tue) 11:30)

「保存する」ということを「観測値が常に一定になる」ことだと定義すると，１つの固有関数だけで表される状態をのぞけば，その物理量は保存しないことになります． しかし，量子力学では「平均値が時間的に一定である」ことを「保存する」と定義しています． この定義によれば，定常状態でエネルギーが保存するのはもちろんですが，定常状態でなくても，ハミルトニアンが時間に陽に依存しない場合は，エネルギーの平均値は一定になるので，エネルギーは保存することになります. 定常状態でない場合は，全く同じ状態であっても異なるエネルギー値が観測されるのだから，古典力学と完全に同じ意味でのエネルギーの保存則が成り立たないのは当然でしょう．

Re: 不確定性原理と無限井戸

まきお さんのレス (2005/07/26(Tue) 21:13)

なるほど，たしかに定常状態のことばっかり考えていました． 同じ状態でも，異なるエネルギーが観測される．それを前提とすれば， そこまで不思議なことではないんですね＾＾ わたしは，渡邊さんが教えてくれたＨＰをみて，少し思ったのですが， 無限に大きなポテンシャルの存在が，粒子に有限のエネルギーを与えるのか と考えました． 色々と新しい発見ができました．この掲示板に来て本当によかったです． yamaさん，渡邊さん，お忙しいところ本当にありがとうございます！ これからも，量子力学の真髄を探していこうとおもいます． この掲示板で，質問に答えれるようになりたいです．どうもありがとう ございました！