力学
力学
ＤＯＴ ＫＩＮＤ さんの書込 (2005/07/24(Sun) 17:34)
Ｑ高さｈの崖の上から斜め上に質量ｍの物体を 初速度v 0 を与えて投げ上げた． このとき物体の水平最大到達距離はいくらか？
という問題でこう考えてみました．
地上を原点として鉛直上方向にｙ軸，水平右方向にｘ軸をとる． v 0 の水平方向とのなす角をθとすると
運動方程式より a x =0 a y =-g
v x =v 0 cos(θ) v y =-gt+v 0 sin(θ)
x=v 0 cos(θ)t・・・（１） y=-(1/2)gt 2 +v 0 sin(θ)t+h・・・（２）
式（２）でｙ＝０となるような時刻ｔ＝toを求めて これを式（１）に代入してx(to)=(θの式)となるので このx(to)を最大にするθを求める そしてこのときのx(to)の値が答えとなる．
このように考えたのですが答えにたどり着きません どこか間違っていますでしょうか？ お願いします．
Re: 力学
ＤＯＴ ＫＩＮＤ さんのレス (2005/07/26(Tue) 12:59)
ｙ＝０となるような時刻ｔを求めたら t=[vo sinθ ＋√((vo sinθ) 2 +2gh)]/g となりました．これを式（１）に代入すると ｘ＝vo cosθ[vo sinθ ＋√((vo sinθ) 2 +2gh)]/g となるんですが，これを２倍角などの公式を使って θを一箇所にまとめるやり方がわかりません． （まとめないとθ＝何でｘが最大か分かりませんよね？) どのような変形をしたら良いでしょうか？
それとも微分して最大値などを求める必要が あるのでしょうか？
Re: 力学
崎間 さんのレス (2005/07/27(Wed) 11:05)
もし崖の上からではなく，水平面での話ならば
という説明から，到達距離を最大にするθは45度だと分かります．
そしてこの条件は，いまの問題の場合（崖の上から投げる）でも 変わらないとして良いと思います． 求めるのは水平最大到達距離ですから， θ=45度を代入して，上で求まっている式を整理してはどうでしょう．
Re: 力学
ｙama さんのレス (2005/07/27(Wed) 12:53)
45度のときに水平到達距離が最大になるのは，あくまでも水平面でのことで，崖の上から投げる場合は，落下までの時間が長くなるので，速度の水平成分が大きくなるように，つまり45度より小さい角度で投げたほうが水平到達距離は長くなると思います． 特に，崖が非常に高い場合，角度を変えても落下までの時間はわずかな割合でしか変わらないので，速度の水平成分の変化が到達距離に大きく影響することになります． その水平到達距離の式ですが，簡単な形にはなりにくそうですね． 微分したほうがいいかもしれません．
Re: 力学
崎間 さんのレス (2005/07/27(Wed) 15:58)
安易な発言で混乱させてしまいました． yamaさん，フォローどうもありがとうございます :)
Re: 力学
RAMSTEIN さんのレス (2005/07/27(Wed) 18:37)
もし，高さｈ下の場所が水平到達とするなら， ｘ＝Ｖ０×ｃｏｓθ×ｔから， 真横（θ＝０°，ｃｏｓ０°＝１）に投げたときが 水平到達距離が最大になるじゃだめですか？
Re: 力学
渡邉 矩章 さんのレス (2005/07/28(Thu) 14:14)
はじめまして．
>もし，高さｈ下の場所が水平到達とするなら， >ｘ＝Ｖ０×ｃｏｓθ×ｔから， >真横（θ＝０°，ｃｏｓ０°＝１）に投げたときが >水平到達距離が最大になるじゃだめですか？
最低，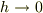 
で 
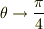とならなければ正しくないと言えると思いますよ．今まで話されてきたとおり極値を探すために微分するのが良いと思いますが，僕は 
が満たす方程式しか分かりませんでした．方程式の解き方はわかりません．
Re: 力学
feder さんのレス (2005/07/28(Thu) 16:35)
どうも，はじめまして．同じ問題を「大学への物理」というページで見たのですが，同じ人かな？それともこの問題，流行っているのでしょうか．
その「大学への物理」さんのところで，実際に，エクセルで計算された方がいるので参考になると思います．
＞RAMSTEINさん tというのは，地面に着いた時の時刻ですよね？残念ながら，tがθに依存してしまうので，θ＝0のとき最大，とはいかないんですよねえ…．
Re: 力学
RAMSTEIN さんのレス (2005/07/28(Thu) 19:15)
> tというのは，地面に着いた時の時刻ですよね？残念ながら，tがθに依存してしまう > ので，θ＝0のとき最大，とはいかないんですよねえ…．
federさん，どうもです． そうなんですか．私なりに勉強を続けていって理解できるようにしてみます．
上記のθとｈを加味したｔ（時間）（私にはまだ意味がよくわかりませんが） を入れた水平距離ｘの式で エクセルで実際に様子をみるのが手っ取り早そうですね．
Re: 力学
渡邉 矩章 さんのレス (2005/07/28(Thu) 19:31)
>上記のθとｈを加味したｔ（時間）（私にはまだ意味がよくわかりませんが）
はじめの方のやり取りを見れば，意味は分かると思いますよ
Re: 力学
ＤＯＴ ＫＩＮＤ さんのレス (2005/07/29(Fri) 11:21)
x=v 0 cos(θ)t・・・（１） y=-(1/2)gt 2 +v 0 sin(θ)t+h・・・（２）
式（１）を式（２）に代入して[ｔ消去] y=-(1/2)(g/v 0 cos 2 (θ))x 2 +tan(θ)x+h
この式が軌道上の点(X.Y)を通るので Y=-(1/2)(g/v 0 cos 2 (θ))X 2 +tan(θ)X+h
ここでtan(θ)=kとおくと Y=-(gX 2 /2v 0 2 )(1+k 2 )+Xk+h
このときY=0となるXの最大値を求める ｋについて整理すると gX 2 k 2 -2v 0 2 Xk-2v 0 h+gX 2 =0
これをｋの方程式とみると，この方程式が実数解をもつ必要があるので 判別式をとりXにつぃて整理すると X≦(v 0 /g)√(v 0 2 +2gh) となり最大到達距離が求まる．
これではダメでしょうか？？ 一応答えにはなるみたいなんですが？
