無題

無題

sin さんの書込 (2005/07/24(Sun) 02:00)

大学で物理を勉強しているsinといいます．

一様な円板（半径a 質量M）が水平面上にあり，その中心を軸に回転できる． 円盤の中心にいる虫（質量ｍ）が初速度０で中心から直径aの円を描いて中心に戻るとき，円盤はどれくらい回転しているか？ という問題があったのですが…

虫の回転角をθ，その反作用での円板の回転角をΦとおいて，円板の回転中心から虫までの距離をｒとおく． 全角運動量は，

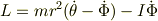
L=mr^{2}(\dot{\theta}-\dot{\Phi})-I\dot{\Phi}

初期条件L=0を代入して，θの変化を 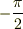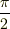-\frac{\pi}{2} 〜 \frac{\pi}{2} として，Φの変化をみて，

\Phi=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{ma^{2}cos^{2}\theta}{ma^{2}cos^{2}\theta+I}d\theta \\=\pi\sqrt[]{\mathstrut \frac{M}{M+2m}}

と計算したのですが，解答とは違いました． でも計算は間違っていないし，考え方も違っていないと思っているのですが…． 間の計算などの詳細は，必要ならばまた記述します． なにがいけないのでしょう？教えてください．

僕の解答が間違っていて，以下に記載する解答が合っている場合， ?の式から積分を実行して，答えにたどり着くまでの積分の経緯（積分の置換の方法とかだけでも…）を一緒に教えていただけるとうれしいです．

本当の解答の詳細を掲載しておきます． (僕の解答ではなく，この問題の本当の解答です．)

円板の水平面上に直径を通る軸をとり，虫の位置を，軸からの距離Rと軸とのなす角θであらわす． 全角運動量は

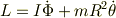
L=I\dot{\Phi}+mR^{2}\dot{\theta}

虫の直径aの円の軌跡の中心から円板の中心へ向かう線分と，軌跡の中心から虫の位置までの線分のなす角をφとする． θとRをそれぞれ，Φとφであらわし，Lを書き換える．

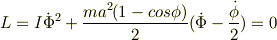
L=I\dot{\Phi}^{2}+\frac{ma^{2}(1-cos\phi)}{2}(\dot{\Phi}-\frac{\dot{\phi}}{2})=0
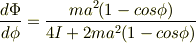
\frac{d\Phi}{d\phi}=\frac{ma^{2}(1-cos\phi)}{4I+2ma^{2}(1-cos\phi)}

・・・? ?を０〜２πの積分として実行して，

\Phi=(1-\frac{1}{\sqrt[]{\mathstrut 3}})\pi

Re: 無題

yama さんのレス (2005/07/24(Sun) 15:18)

あなたの解答も「本当の解答」もどちらも間違っています． 虫の質量 m が非常に小さい場合は，円盤はほとんど回転しないので，Φ は 0 に近づくはずですが，どちらの解答も m→0 のとき 0 には近づきません． 特に，「本当の解答」で Φ が定数になっているのはおかしいと思います． あなたの解答と「本当の解答」は，角度の取り方が違いますが，途中までは一致しているようです． あなたの解答の積分の式で θ を π/2-φ/2 で置き換えて φ で微分すると，「本当の解答」の?式の符号を変えたものになるからです．符号が変わるのは Φ の向きの取り方が違うためです．

Re: 無題

sin さんのレス (2005/07/24(Sun) 19:24)

回答ありがとうございます． たしかに，ｍ→０でΦ→０でないのは，おかしいですね…． 気づきませんでした． この問題を考えたとき，この解答のやり方しか思いつかず， 自分が解いたものの何が違うのかまったくわからないのですが…． 正しい答えを導くには， どのような指針で解いていったらよいのでしょう？

Re: 無題

yama さんのレス (2005/07/24(Sun) 20:32)

積分で表すところまでは合っていると思います． m=0 のときの積分値は明らかに 0 になることがわかりますが，あなたの計算結果を用いれば π になってしまいます．つまり積分の計算が間違っているということです．

Re: 無題

sin さんのレス (2005/07/24(Sun) 23:12)

できました． ありがとうございました．