物理数学
物理数学
みっちー さんの書込 (2005/07/19(Tue) 18:50)
テスト勉強していたら判らない所があったので・・
ベクトルVが以下のように与えられている時それぞれのdivVおよびrotVを求めよ. ただしaは定数,cは定数ベクトル,ベクトルr=xi+yj+zk ,r=|r|である.
?V=ar ?V=C×r ?V=r/rの三乗 ?V=C/r divV=∇VでrotV=∇×Vというのはわかります. この二つの式の違いはrotのほうはベクトルの外積ってことですよね? ?だとdivV=div(ar)=∇(ar)でaが定数だから前に出てa∇rになって ∇=(d/dx,d/dy,d/dz)となってそれぞれ微分されてaがのこり3aとなる. こんな感じでよいのでしょうか? ?はCの定数ベクトルの扱いをどうしてよいかわからなくて..
Re: 物理数学
みっちー さんのレス (2005/07/19(Tue) 21:15)
公式は覚えなくて良いといわれたんですが覚えなくて良いのでしょうか?
Re: 物理数学
toorisugari no Hiro さんのレス (2005/07/19(Tue) 23:19)
まず,記法を正確に覚えましょう. ベクトルとスカラをきちんと区別しましょう.
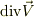 は
は 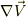 でなく
でなく 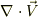 です.
です.
(1)の問題はV=arと書いていますが,rはスカラ  なのかベクトル
なのかベクトル 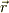 なのかわかりません.おそらく
なのかわかりません.おそらく  でなく
でなく 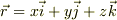 のはずです.ここら辺を混同していたら問題は解けませんので,まずそこをいい加減にしないでください.(
のはずです.ここら辺を混同していたら問題は解けませんので,まずそこをいい加減にしないでください.( 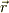 がかけないならvec{r}でも通じます.)まず,問題を正しく表記するところから始めましょう.
がかけないならvec{r}でも通じます.)まず,問題を正しく表記するところから始めましょう.
 ,
, 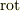 ,
, 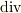 の定義(直交座標系での成分演算方法)を理解していれば,計算は難しくないはずです.
の定義(直交座標系での成分演算方法)を理解していれば,計算は難しくないはずです.
ただ,きちんと微分のルール(積の微分,入れ子の微分)を理解していないと 難しいかな?
公式としては 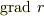 を覚えていれば便利かなってぐらいです.
それよりまず,暗記でなくきちんとルール通りに計算できることが先決.
を覚えていれば便利かなってぐらいです.
それよりまず,暗記でなくきちんとルール通りに計算できることが先決.
Re: 物理数学
toorisugari no Hiro さんのレス (2005/07/20(Wed) 20:34)
> 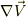 は
は 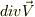 ではなくて
ではなくて 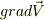 を表すんでしたっけね?
を表すんでしたっけね?
そうです. 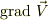 はテンソルとしての意味を持ちますが,初学者の人は,間違った使い方と考えていいでしょうね.
はテンソルとしての意味を持ちますが,初学者の人は,間違った使い方と考えていいでしょうね.
 はスカラをベクトルに
はスカラをベクトルに
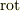 はベクトルをベクトルに
はベクトルをベクトルに
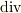 はベクトルをスカラに
はベクトルをスカラに
対応させるものだと考えるべきです.
なお,これらの正確な定義はガウスの定理やストークスの定理の表面積分(周積分)の密度(面密度)であると考えるのがよいと思います.
Re: 物理数学
やかん さんのレス (2005/07/21(Thu) 12:14)
>そうです. 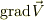 はテンソルとしての意味を持ちますが,初学者の人は,間違った使い方と考えていいでしょうね.
はテンソルとしての意味を持ちますが,初学者の人は,間違った使い方と考えていいでしょうね.
あっ,間違えました.偏微分演算子に演算させるのは勾配の場合,スカラーでしたね.
>  はスカラをベクトルに
はスカラをベクトルに
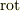 はベクトルをベクトルに
はベクトルをベクトルに
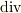 はベクトルをスカラに
はベクトルをスカラに
対応させるものだと考えるべきです.
なお,これらの正確な定義はガウスの定理やストークスの定理の表面積分の(面)密度であると考えるのがよいと思います.
なるほど・・・.本を読んでいて知っていたはずが,やはりちゃんとわかっていなかったのでとても勉強になりました.toorisugari no Hiroさん,有難うございました.
Re: 物理数学
みっちー さんのレス (2005/07/21(Thu) 13:06)
勉強してみて指摘されたとおりそもそもベクトル自体の知識があいまいだったようです. スカラーとベクトル,内積t
Re: 物理数学
みっちー さんのレス (2005/07/21(Thu) 13:08)
勉強してみて指摘されたとおりそもそもベクトル自体の知識があいまいだったようです スカラーとベクトル,内積と外積の以外などです.. おかげさまでテスト結構できました.. もう1つの範囲の複素積分はけっこうできたんですけど ベクトルがどうしてもできなくて・・.. でもだいぶわかるようになりました.ありがとうございます.
Re: 物理数学
みっちー さんのレス (2005/07/21(Thu) 13:08)
前の間違いです..2重投稿すいません..