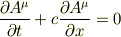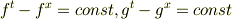無題

無題

isuzu さんの書込 (2005/07/16(Sat) 07:26)

連続して質問になってすみません． 同じく電磁気分野なのですが…．

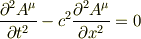
\frac{\partial^{2} A^{\mu}}{\partial t^{2}}-c^{2}\frac{\partial^{2} A^{\mu}}{\partial x^{2}}=0

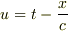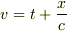を，遅延時間 u=t-\frac{x}{c} ，先進時間 v=t+\frac{x}{c} をつかって一般解を求めるとき，uとvで上式を変形して，

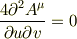
\frac{4\partial^{2}A^{\mu}}{\partial u \partial v}=0

という条件式まで出しました． ここから，一般解はどう出せばいいのですか？

Re: 無題

yama さんのレス (2005/07/16(Sat) 11:16)

μを省略して書くと (∂/∂u)(∂A/∂v)=0 なので∂A/∂v は v だけの関数になります．これを h(v) とおくと ∂A/∂v=h(v) となるのでvで積分すると A=∫h(v)dv+g(u) となります．「積分定数」は u の任意関数 g(u) です． ∫h(v)dv=f(v) とおくと結局 A=f(v)+g(u) となります．f,g は任意の関数です．

Re: 無題

isuzu さんのレス (2005/07/16(Sat) 15:11)

では，一般解はローレンツゲージ条件

\frac{\partial A^{\mu}}{\partial t}+c \frac{\partial A^{\mu}}{\partial x} = 0

を含めると,

f^{t}-f^{x}=const,g^{t}-g^{x}=const

になるのですね． わかりやすかったです，ありがとうございます．

Re: 無題

yama さんのレス (2005/07/16(Sat) 21:25)

その式はローレンツゲージ条件の式ではないと思いますが・・・ ローレンツゲージ条件は，波動方程式を導く過程ですでに適用しています． １次元波動方程式の一般解は A=f(t+x/c)+g(t-x/c) です．互いに反対方向に進む波の重ね合わせになっています．

Re: 無題

みぃ さんのレス (2005/07/18(Mon) 15:13)

おひさしぶりです． 横レス，すみません． この問題を見て，考えてて疑問に思ったのですが…． この条件で出た解は， ｘ軸方向に伝わる平面波を考えたとき，

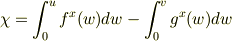
\chi=\int_{0}^{u}f^{x}(w)dw-\int_{0}^{v}g^{x}(w)dw

というゲージ変換で，

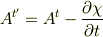
A^{t'}=A^{t}-\frac{\partial \chi}{\partial t}
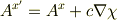
A^{x'}=A^{x}+c\nabla\chi

を計算して，

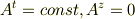
A^{t}=const,A^{z}=0

とすることができますよね？ ここの積分式のゲージ変換は，どうやって決めてるんですか？ 今まで，こういうときはこれを使うもんだって，天下り的にやってたのですが， いざ考えてるとどうやって出しているのか，考えても分かりませんでした． 教えてください．

なお，u,vはisuzuさんの定義に従ってます．

あと…No.6095の記事のローレンツゲージ条件なんですが， あれって，ローレンツゲージ条件じゃないんですか？？

似たような問題で，ｘ軸方向に電場する平面波Aを考えると，マクスウェル方程式をローレンツゲージ条件の下で書き直した式はNo.6091の一番最初の式になって， ローレンツゲージ条件はNo.6095の式になるというような問題文を見たことがあるのですが…．（←言ってることが分かりにくいかもしれませんが…すみません．）

Re: 無題

みぃ さんのレス (2005/07/18(Mon) 22:02)

横レスとか…めっちゃ失礼でしたかね…(^^; そうだとしたらすみません．

Re: 無題

yama さんのレス (2005/07/18(Mon) 23:50)

失礼ではないと思いますが・・・ そのゲージ変換の式がどこから出てきたかはよく分りません． No.6095の式は，同じ成分についてtとxで微分している点で，ローレンツゲージ条件とは違うように思います． 平面波の場合はNo.6095の式になるのかもしれませんが，そのあたりもよく分りません