特殊相対論

特殊相対論

玲 さんの書込 (2005/07/14(Thu) 00:46)

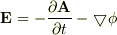
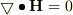
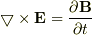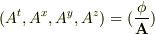はじめまして，物理科の大学生の玲(あきら)です． 特殊相対論の問題で， 「電場Eと磁束密度BはスカラーポテンシャルΦとベクトルポテンシャルAを用いて， {\bf E} = - \frac{\partial \bf A}{\partial t} - \bigtriangledown \phi {\bf B} = \bigtriangledown \times {\bf A} と表すことができる．以下の問いに答えよ． (a)上記のようにEとBをΦとAで表すと，マクスウェル方程式， \bigtriangledown \bullet {\bf H} = 0 \bigtriangledown \times {\bf E} = \frac{\partial {\bf B}}{\partial t} が自明に満たされることを示せ． (b)四元電磁ポテンシャルの {\cal O} 系での成分は， (A^{t}, A^{x}, A^{y}, A^{z}) = (\frac{\phi}{{\bf A}}) と定義される．ローレンツ変換により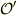， {\cal O}' 系でのΦ’とA'を速さVと 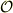{\cal O} 系の成分で表せ． (c)(b)の結果を用いて， {\cal O}' 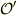系での電場E'と磁束密度B’を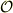， {\cal O} 系の電場Eと磁束密度Eと速さVで表せ．」

というのがありました． (b)の問題は，

\frac{\phi'}{c} = \frac{\frac{\phi}{c}-V{\bf A}}{\sqrt[]{\mathstrut 1-V^{2}}}{\bf A}' = \frac{{\bf A}-V\frac{\phi}{c}}{\sqrt[]{\mathstrut 1-v^{2}}}

と考えました．あっていますか？

(a)(c)については，何をどう解いていったらよいのか分かりません． どなたかご教授ください．お願いします．

Re: 特殊相対論

渡邉　矩章 さんのレス (2005/07/14(Thu) 07:47)

はじめまして．

>(a)上記のようにEとBをΦとAで表すと，マクスウェル方程式， ファラデーの法則（式） >が自明に満たされることを示せ

これは，問題ミスですよね（正しくは∇×Ｅ＝−∂Ｂ/∂ｔ）？これはベクトルの公式を見ながらやればできると思います．

Re: 特殊相対論

玲 さんのレス (2005/07/15(Fri) 04:42)

はい，間違いです．すみません． 二つ目マクスウェル方程式（EとBに関するもの）のベクトル式のを計算してみたいのですが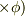， ∇(∇ \times \phi) がゼロにるのはどうしてですか？

Re: 特殊相対論

yama さんのレス (2005/07/15(Fri) 07:29)

成分で表して計算してみればわかります． 当然ながら，２階偏微分で偏微分の順番は交換できるとします．

Re: 特殊相対論

玲 さんのレス (2005/07/15(Fri) 18:47)

その計算については理解できました． ベクトル計算が，かなり苦手なようです・・・． ありがとうございました．