変数分離型微分方程式
変数分離型微分方程式
蛍 さんの書込 (2005/07/12(Tue) 20:05)
はじめまして.蛍といいます. 大学1年生で,高校で物理を履修していません. 大学では物理未履修者クラスに入っているのですが,授業で出されたレポート問題が分からないので,質問させてください. 教授が5分くらい微分方程式について語り,「じゃあこの3つレポートにしてきてね」といっただけでほとんど知識もなく,困っています.
「xdy/dx=y^2-1(yの2乗マイナス1)を解け」
∫dy/(y^2-1)=∫dx/x (yは±1以外,xは0以外) 1/2∫(1/(y-1)-1/(y+1))dy=loglxl+C logl(y-1)/(y+1)l=2loglxl+C ここまで解いてみたのですが,y=の形に出来ません・・・.
Re: 変数分離型微分方程式
篠原 さんのレス (2005/07/12(Tue) 20:41)
蛍さん,はじめまして. 篠原と申します.
最後の式の両辺の対数をとります. その後に,両辺に(y+1)をかけて・・・ とすると,わかると思います.
大変そうですね.がんばってください!
Re: 変数分離型微分方程式
蛍 さんのレス (2005/07/12(Tue) 21:20)
篠原さん,レスありがとうございます. また質問なのですが,絶対値記号はつけたままで,両辺に(y+1)をかけるのでしょうか?
Re: 変数分離型微分方程式
篠原 さんのレス (2005/07/12(Tue) 22:06)
対数ではなく,指数ですね.間違いましたごめんなさい. 絶対値のことを,忘れていました・・・ 右辺のxについては,2乗になるので,絶対値を無視してもかまわないでしょう. 左辺については,確かに無視できないのですが,
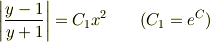
と置いたとき,本来 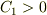 になるのですが,
この
になるのですが,
この 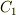 を,実数全体の値をとり得ると考えれば,
言い換えれば,絶対値を取る代わりに,
を,実数全体の値をとり得ると考えれば,
言い換えれば,絶対値を取る代わりに, 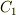 が負の値もとり得ると考えれば,左辺についての絶対値を無視していいでしょう.
が負の値もとり得ると考えれば,左辺についての絶対値を無視していいでしょう.
Re: 変数分離型微分方程式
蛍 さんのレス (2005/07/13(Wed) 00:22)
どうもありがとうございます. この問題の答ですが, y=(1±e^c・x^2)/(1マイナスプラスe^c・x^2) となりました. (コマンドが使いづらかったので直接打ち込みました.分かりにくくてすみません) コレでいいんでしょうか・・・
それと,もう2つ問題があって, ydy/dx=−x (1+x)dy/dx=1−y
なのですが,前者の計算が, (1/2)y^2=(-1/2)x^2+C となり,コレでいいのか迷ってしまい,後者は, y=1±e^c(1+x) という答が出たのですが自信がありません. よろしければアドバイスをください.
Re: 変数分離型微分方程式
FKD さんのレス (2005/07/13(Wed) 01:00)
微分方程式の計算結果に自信がないときは
求まった答えから 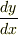 などを求めて
元の式に代入すると検算ができますよ.
などを求めて
元の式に代入すると検算ができますよ.
Re: 変数分離型微分方程式
蛍 さんのレス (2005/07/13(Wed) 07:48)
ありがとうございます. ydy/dx=−xの計算が (1/2)y^2=(-1/2)x^2+C という所まで進んだのですが,ここから答を出していいのでしょうか.
Re: 変数分離型微分方程式
篠原 さんのレス (2005/07/13(Wed) 09:42)
そこまではあってます. ただ,y=… の形にした方がいいでしょう. ただし,全ての微分方程式で,y=f(x)の形に出来るわけではないので,その場合は出来るだけ簡単な形の式で答えましょう.
Re: 変数分離型微分方程式
篠原 さんのレス (2005/07/13(Wed) 10:09)
あぁ,円の方程式ですね… x^2+y^2=r の形で答えたほうがいいかもしれませんね. すいません.
Re: 変数分離型微分方程式
蛍 さんのレス (2005/07/13(Wed) 21:43)
こんばんは. 最初から問題を解きなおしてみたところ, (1)y=(1±e c x 2 )/(1干e c x 2 )(複号同順) (2)x 2 +y 2 =α(αは定数) (3)y=1±e 2 /(1+x) となりました. 微分して代入すると,どれももとの式が成立したのですが,±が出てきたりしていまいち自信が持てません. コレでいいのでしょうか?
上の投稿の(3)
蛍 さんのレス (2005/07/13(Wed) 21:45)
y=1±e c /(1+x)の間違いです.すみません.
では
蛍 さんのレス (2005/07/14(Thu) 22:21)
(1)y=(1+C)/(1-C) (2)x2+y2=α(αは定数) (3)y=1+C/(1+x) (C=±e c ) でよろしいでしょうか.
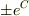 をあらためて
をあらためて 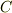 とおき直すと
とおき直すと