ガウス定理とストークス定理
ガウス定理とストークス定理
Κ さんの書込 (2005/07/12(Tue) 01:05)
こんばんは.質問が二つあります.
1,全空間で定義されたベクトル場Aに対して,  となるベクトル場Bがあれば,任意の閉曲面Sについて
となるベクトル場Bがあれば,任意の閉曲面Sについて 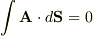 となることを示せ.
自分では,ガウスの定理より
となることを示せ.
自分では,ガウスの定理より  とやったのですが,あっていますでしょうか?解答ではストークスの定理を使ってといていたので.
2,発散は「流体が一秒間に湧き出す体積密度」と具体的な例がありますが,回転は本を調べても,「渦の強さを表すと考えられる」とか「渦を表す」とか,曖昧なことしか書いてないのですが,具体的なイメージはないのでしょうか?
とやったのですが,あっていますでしょうか?解答ではストークスの定理を使ってといていたので.
2,発散は「流体が一秒間に湧き出す体積密度」と具体的な例がありますが,回転は本を調べても,「渦の強さを表すと考えられる」とか「渦を表す」とか,曖昧なことしか書いてないのですが,具体的なイメージはないのでしょうか?
Re: ガウス定理とストークス定理
篠原 さんのレス (2005/07/12(Tue) 02:06)
Kさん,はじめまして.篠原と申します.
- あっている.(と思います・・・)
- 回転は非常にイメージしにくいのですが,あるベクトル場の中のある位置に,微小な閉じたホースのような筒状の空間を考えます.ベクトルを水の流れのように考え,ある瞬間,その筒状の空間の外側の水を一瞬で凍らせ,そのホースの内側の水の流れだけについて考えたとき,ホースの右側の"流れ"が左側の"流れ"より強かった場合,ホースの中には反時計方向に水が流れることになります.このように,微小なホースの中に"流れ"が存在する場合,その位置でのベクトル場の回転は,ホースの法線方向成分について0でなくなる.というのが,私なりの回転の解釈の仕方です.
Re: ガウス定理とストークス定理
yama さんのレス (2005/07/12(Tue) 09:02)
回転する剛体の任意の点の速度の「回転」は,剛体が回転する角速度の2倍に等しくなります. これが「回転」の由来だそうです.
Re: ガウス定理とストークス定理
やかん さんのレス (2005/07/12(Tue) 13:10)
Kさん,こんにちは! 以前私もこちらで”回転”を質問させていただいた事があるのですが その時いただいた崎間さんのご説明がとってもわかりやすかったので ご紹介いたします.あと以前読んだ本には,2次元で考えると,軸方向に長さのある軽く回る歯車を水流につけたとき,回りだせば(渦があれば),回転の値(rot)がゼロでない.それからもう一つ,ある点から出発して,そこいらをぐるっと一周して,元の点に戻る時,流れを下ったり,上ったりで,線積分値は合計ゼロになるけど,渦(回転)があれば,それに乗っかって楽できるから,ゼロにならない.逆に言うと,周回線積分値がゼロでなければ,回転がある,と書いてありました(ほとんど受け売りです).
Re: ガウス定理とストークス定理
Κ さんのレス (2005/07/16(Sat) 21:56)
返信遅れて申し訳ありません.たくさんのレスありがとうございます.
イメージはわかったのですが,もっと厳密的な定義,数式から導かれる意味のようなものはないでしょうか?
>回転する剛体の任意の点の速度の「回転」は,剛体が回転する角速度の2倍に等しくなります
詳しく教えていただけないでしょうか?自分の調べた本ではxy平面上では 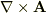 が角速度を表すという証明がのっていました.
が角速度を表すという証明がのっていました.
Re: ガウス定理とストークス定理
Joh さんのレス (2005/07/16(Sat) 22:31)
微分係数を傾きとして,x-y平面上で,二次元の回転を描いてみるといいと思いますよ.
Re: ガウス定理とストークス定理
yama さんのレス (2005/07/17(Sun) 00:51)
剛体の重心の座標を  とし,重心の(並進運動の)速度を
とし,重心の(並進運動の)速度を  とし,回転の角速度を
とし,回転の角速度を 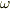 とします.
剛体の任意の点の座標を
とします.
剛体の任意の点の座標を  ,その点の速度を
,その点の速度を  とすると
とすると
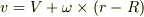 という関係が成り立ちます.詳しくは,力学の本を見てください.
この回転を計算すると
という関係が成り立ちます.詳しくは,力学の本を見てください.
この回転を計算すると
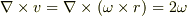 となります.成分で表して計算してみれば確かめられます.
つまり,速度の回転が角速度の2倍になるわけです.
となります.成分で表して計算してみれば確かめられます.
つまり,速度の回転が角速度の2倍になるわけです.
Re: ガウス定理とストークス定理
Κ さんのレス (2005/07/21(Thu) 01:42)
ありがとうございます.まだ空間での力学を勉強してないので,レスを参考に勉強します.遅れてすみませんでした.
Re: ガウス定理とストークス定理
toorisugari no Hiro さんのレス (2005/07/21(Thu) 17:32)
> もっと厳密的な定義,数式から導かれる意味のようなものはないでしょうか?
別のスレッドでもふれていますが,  ,
, 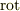 ,
, 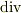 の定義(意味)は積分で考えるべきですね.
ガウス-ストークス-グリーンの定理を列挙すると
(1)
の定義(意味)は積分で考えるべきですね.
ガウス-ストークス-グリーンの定理を列挙すると
(1)
![\int_L \mbox{grad} f \cdot \mbox{d}\vec{r} = \oint_{\partial L} f ~(\equiv [f(\vec{x})]_{\vec{a}}^{\vec{b}})](http://hooktail.maxwell.jp/bbslog/473fa4b9d0889390864216a02a5525db.png)
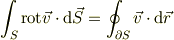
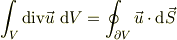
( 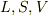 は三次元空間内での曲線,曲面,領域を表し,
は三次元空間内での曲線,曲面,領域を表し, 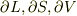 はその境界を表します.
はその境界を表します. 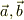 は
は 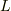 の始点と終点です.)
となりますが,これを定理と考えるよりも
の始点と終点です.)
となりますが,これを定理と考えるよりも  ,
, 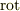 ,
, 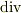 の定義と考えるべきですね.
の定義と考えるべきですね.
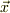 を含む微小体積
を含む微小体積 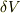 を考えると体積積分は関数×体積と近似できるので(3)は
を考えると体積積分は関数×体積と近似できるので(3)は
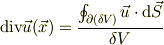
となります. 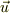 を流体の速度と考えれば,「発散」とは「微小領域から単位時間あたりわき出る体積」を「微小領域の体積」で割ったもの,すなわち微小領域にある流体の「流れによる体積膨張率(密度)」を表します.
を流体の速度と考えれば,「発散」とは「微小領域から単位時間あたりわき出る体積」を「微小領域の体積」で割ったもの,すなわち微小領域にある流体の「流れによる体積膨張率(密度)」を表します.
「回転」は(2)の積分からイメージするのは難しいですが,
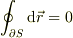 ,
, 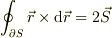 ,
, 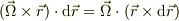 であることから,流れが角速度
であることから,流れが角速度  の剛体運動(
の剛体運動(  :
: 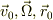 は定ベクトル)をしてるならば,微小面要素
は定ベクトル)をしてるならば,微小面要素  において
において
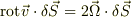 すなわち
すなわち
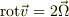 となり,剛体回転成分(微小要素の自転)の角速度の2倍が「回転」です.前の方でもあげられているように,流体に微小な水車を差し込んで,最大角速度の回転をするときの,軸の右ねじ進行方向を「方向」,回転の角速度の2倍を「大きさ」に持つ「ベクトル」が「回転」であると考えてもいいです.
となり,剛体回転成分(微小要素の自転)の角速度の2倍が「回転」です.前の方でもあげられているように,流体に微小な水車を差し込んで,最大角速度の回転をするときの,軸の右ねじ進行方向を「方向」,回転の角速度の2倍を「大きさ」に持つ「ベクトル」が「回転」であると考えてもいいです.
「傾き」は曲線として微小な線素 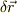 を考えれば,
を考えれば, ![[f]_{\vec{r}}^{\vec{r}+\delta\vec{r}} = \delta f](http://hooktail.maxwell.jp/bbslog/4fd172f0bd2929402b7e45da60a46ae7.png) ですから,(1)の積分より
ですから,(1)の積分より
 となり,一次元の傾きの概念「道のり(の水平成分)×傾き=高さ」を素直に拡張したものになります.(あるいは線素
となり,一次元の傾きの概念「道のり(の水平成分)×傾き=高さ」を素直に拡張したものになります.(あるいは線素 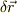 をいろいろ変えて,もっとも
をいろいろ変えて,もっとも 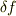 が大きいときの「方向」とそのときの傾き
が大きいときの「方向」とそのときの傾き 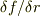 を「大きさ」にもつベクトルと考えてもいいです.)
を「大きさ」にもつベクトルと考えてもいいです.)
積分で考えると極座標での 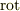 とかが簡単に計算できるメリットもあります.
とかが簡単に計算できるメリットもあります.
Re: ガウス定理とストークス定理
Κ さんのレス (2005/07/23(Sat) 00:08)
僕も実際に計算をしたりするときは toorisugari no Hiroさんのおっしゃるようなイメージで覚えているのですが,鶏が先か,卵が先かみたいな感じがしませんか? この前テストでストークスの定理を導け,という問題で上のような「積分で考えた意味」を定義として,それが一般に対して成り立つことだけを証明したのですがあってるかわかりません.
Re: ガウス定理とストークス定理
toorisugari no Hiro さんのレス (2005/07/23(Sat) 05:41)
H>  ,
, 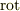 ,
, 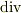 の定義(意味)は積分で考えるべきですね.
K> 鶏が先か,卵が先かみたいな感じがしませんか?
の定義(意味)は積分で考えるべきですね.
K> 鶏が先か,卵が先かみたいな感じがしませんか?
確かにそうです.要はどこを出発点にすると便利になるかということだと思います.積分で考えた方が物理的/幾何学的意味がつかみやすく,一般座標系での計算が自然にできるので私は上述の考え方を選択しています.
私はガウス-ストークス-グリーンの定理の定理たる部分は微分形式
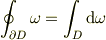
だと思います.
これは,2つの事柄を意味すると考えます.すなわち,
- 単連結な領域
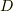 がふたつの単連結な領域
がふたつの単連結な領域 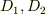 に分割できる,すなわち,
に分割できる,すなわち, 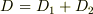 なら,そこでの「表面」積分は相加性
なら,そこでの「表面」積分は相加性
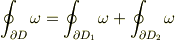
がなりたつ(∵ 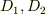 の境界の「表面」積分の寄与は打ち消しあう).
(従って,
の境界の「表面」積分の寄与は打ち消しあう).
(従って, 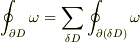 )
)
- 十分小さな領域
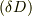 での「表面」積分は被積分要素の「微分」である.
での「表面」積分は被積分要素の「微分」である.
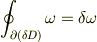
((1)より 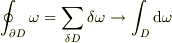 )
)
です. ((2)を微分の定義だとすれば(1)の「表面積分は相加性をもつ」だけが定理です.)
1次元で説明しましょう.
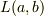 を区間
を区間 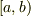 ,
, 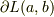 を
を 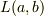 の始点と終点,とします.また,
の始点と終点,とします.また, 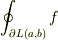 は
は ![[f]_a^b=f(b)-f(a)](http://hooktail.maxwell.jp/bbslog/2302444cacb7fa635a8cfcd321d36bf3.png) を意味するとします.
を意味するとします.
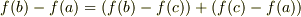 ですから
ですから
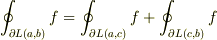 です.(1)
です.(1)
また,  です.(2)
です.(2)
よって, 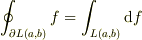 がえられます.
がえられます.
すなわち(1)(2)は一次元でのスカラ関数を考えるときにはなじみの話
![[f(x)]_a^b = \int_a^b \mbox{d}f(x)](http://hooktail.maxwell.jp/bbslog/38696e6edd851032c2aa994e2b97f2ef.png) です.
です.
定理のすごいところは,これが,次元によらず,また, 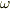 が任意の微分形式(ベクトルだろうがスカラだろうが)で,成り立つと言いきったところだと思います.
(多様体とかをきちんと理解してるわけではないので,あくまでも私個人の理解です.)
が任意の微分形式(ベクトルだろうがスカラだろうが)で,成り立つと言いきったところだと思います.
(多様体とかをきちんと理解してるわけではないので,あくまでも私個人の理解です.)
そしてこの微分形式であらわされた定理とは独立に「微分係数の定義」があると考えます.(本当に独立なのかは自信がないです.)
すなわち,
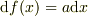 となるような係数
となるような係数  が存在し,これを
が存在し,これを 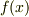 の
の  微分
微分 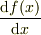 とよびます.
とよびます.
これをベクトルの面績分の場合で言い換えれば
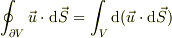 がなりたち,(ただし,
がなりたち,(ただし, 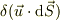 とは
とは 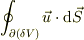 を意味します.)
を意味します.)
 となるような微係数
となるような微係数  を
を 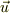 の発散(
の発散( 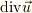 )とよびます.
)とよびます.
となります.これらを一つの式で言い換えたものがガウスの定理,という理解です.相加性はある意味自明なので,ガウスの定理は発散の定義になります.
ちなみに  ,
, 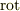 ,
, 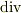 の「微分形での定義」は
の「微分形での定義」は

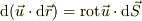
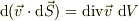 となります.
となります.
もし,試験で「ガウスの定理」を証明せよ,ということなら,相加性により微小領域で考えればばいいので,そこでの表面積分
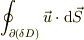 を直交座標系で計算して(もちろんそのときは領域は直方体に採ります.),その値が
を直交座標系で計算して(もちろんそのときは領域は直方体に採ります.),その値が
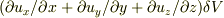 となることを示せば「証明」になるのでは?
(もちろん,これは
となることを示せば「証明」になるのでは?
(もちろん,これは 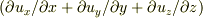 が
が 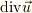 だと「定義」されている場合です.私なら相加性を示して証明したことにします.)
だと「定義」されている場合です.私なら相加性を示して証明したことにします.)
長文お許しください.