るい さんの書込 (2005/07/11(Mon) 22:07)

以下が正準変換となるa，bの値を求めよ． Q = 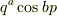P =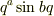

という問題があるのですが，いったい何の式を使ってやったらいいのか， さっぱり分かりません． どなたか，指針を教えてください． お願いします．

yama さんのレス (2005/07/11(Mon) 22:41)

正準変換となる条件は，ポアッソン括弧を用いて {PQ}=1 で表されます．

るい さんのレス (2005/07/12(Tue) 20:05)

返信，ありがとうございます． yamaさんの書いてくださった条件式を， {PQ}= 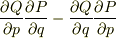= =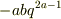1 と計算したのですが…． この計算はあっていますか？？

この式からaとbの値を決定できるのですか？

yama さんのレス (2005/07/12(Tue) 22:56)

まず初めにお詫びして訂正しておきます． 正準変換の条件は {PQ}=1 じゃなくて正しくは {QP}=1 でした．

計算してみたところ{QP}は簡単な式にはなりません． ひょっとすると P=(q^a)sin bp の間違いではないでしょうか．その場合は {QP}=abq^(2a-1) になります． 条件 {QP}=1 は恒等式なので q^(2a-1) は定数でないといけません． これからaが求まり，続いてbも求まることになります．

るい さんのレス (2005/07/12(Tue) 23:35)

確かに，式が間違っていたみたいです． すみません…． 無事，aとbを求めることができました．

そこで新しく疑問なのですが，この問題の場合のポアソン括弧の正しい表式は， {QP}= 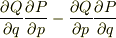ですよね．

このポアソン括弧を最初に計算したとき，一応教科書の公式を見ながら変換したのですが， {QP}= 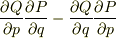としてしまいました． その結果，計算した{QP}がマイナスになっていたようです．

この変分の順はどうやって決めたらいいのですか？

yama さんのレス (2005/07/13(Wed) 00:25)

前のNo.6026では{PQ}がマイナスになっているので，間違っていたわけではありません． なお，普通の定義とp,qの順番を逆にしたポアッソン括弧の定義も一部では用いられているようです．その場合，一般的な定義と符号が違ってきます．

るい さんのレス (2005/07/14(Thu) 00:18)

では，｛PQ｝のときはｐの変分×ｑの変分で，｛QP｝のときはｑの変分×ｐの変分が第一項の掛け算の順だと覚えていたらよいのですか？？

ｙama さんのレス (2005/07/14(Thu) 09:40)

どちらの場合もｑの変分×ｐの変分が第一項です． 一般に {fg}=∂(f,g)/∂(q,p) です． 従って {QP}=∂(Q,P)/∂(q,p) {PQ}=∂(P,Q)/∂(q,p) となります． あるいは，量子力学の交換子 [f,g]=fg-gf に対応させて憶えるといいでしょう．