はじめまして.
はじめまして.
清 さんの書込 (2005/07/11(Mon) 11:00)
はじめましてこんにちは. 自分は大学1年生です. 課題で,球突きの問題が出たんですが,球を突く高さlが7a/5以上か以下かで回転の仕方が変わってくるらしいんですが,この7a/5と言う数字がどの教科書を見ても書いてあるんですがこの値はどのような根拠?(実験)で決められた値なんですか?わかる方がいたら教えてくださいお願いしますm(_ _)m ちなみに注意書きとは違うんですが l>7a/5の場合はv'o=vo-aωo<0となると書いてあります.
Re: はじめまして.
yama さんのレス (2005/07/11(Mon) 11:36)
球が滑らずに転がるときは,並進運動の速さvは外周部の回転速度aωに等しいわけですが,滑りがあるときはv<aωかv>aωかで,摩擦力の向きが違うので回転のしかたが違ってきます. どちらになるかが突く高さによって決まるのでしょう. 並進と回転の運動方程式を解けばわかると思いますが,球の慣性モーメント(2/5)Ma^2が関係してくるでしょう.
Re: はじめまして.
清 さんのレス (2005/07/11(Mon) 12:20)
yamaさんありがとうございます. 球の慣性モーメント(2/5)Ma^2が関係してくるところはなんとかたどりつきました.なんですが,それで,なぜl>7a5が基準なのかがわかりません:;
Re: はじめまして.
FKD さんのレス (2005/07/11(Mon) 12:57)
清さん,yamaさんこんにちは,
球の質量を  ,球を突く激力の力積を
,球を突く激力の力積を 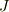 ,球の初速度を
,球の初速度を 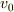 とすると運動量保存則より
とすると運動量保存則より
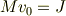
となります.
また,球の慣性モーメントを 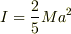 ,球の半径を
,球の半径を  ,球を突く高さを
,球を突く高さを 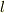 とすると
球の回転しだす際の角速度
とすると
球の回転しだす際の角速度 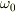 は
は
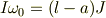
であらわされます.
ここで,球が地面に接しているところにおける,
回転のための速度の大きさは 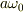 ですから,
球が地面に対して滑る速さ
ですから,
球が地面に対して滑る速さ 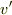 は
は
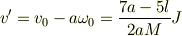
となり,この 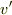 の正負を考えるところから
の正負を考えるところから
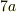 と
と 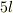 ,
すなわち
,
すなわち 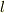 と
と 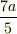 の
大小を考えることにつながる訳です.
の
大小を考えることにつながる訳です.
(岩波の「力学」(戸田盛和著)の180-181ページを参考にしました.)
Re: はじめまして.
清 さんのレス (2005/07/11(Mon) 15:12)
FKDさんありがとうございましたm(_ _)m なんとなくですけど理解できたような気がします. yamaさんご協力ありがとうございましたm(_ _)m
Re: はじめまして.
清 さんのレス (2005/07/12(Tue) 11:31)
FKDさんすみません. ちょっと一番最後のv'の式からこのv'の正負を考えるところから7aと5L,すなわちLと7a/5の大小を考えることにつながると言うところなんですが, v'の正負を考えるところから7aと5LだけをくりぬきLと7a/5の大小を考えることになるんでしょうか? お手数ですが教えてください.お願いしますm(_ _)m
Re: はじめまして.
CO さんのレス (2005/07/12(Tue) 12:42)
いま, 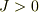 ,
, 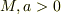 で,
で, 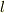 が自分で調節できるパラメータなので,
が自分で調節できるパラメータなので, 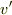 の正負を考えるとき
の正負を考えるとき 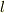 が
が 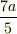 より大きいか小さいかでわけるのではないでしょうか.
より大きいか小さいかでわけるのではないでしょうか.
Re: はじめまして.
FKD さんのレス (2005/07/12(Tue) 13:12)
COさんのおっしゃるとおりです.