面積分の問題
面積分の問題
Κ さんの書込 (2005/07/10(Sun) 00:33)
こんばんは.質問があるのでお願いします.
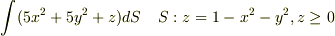 を面積分せよ.
自分の解答
を面積分せよ.
自分の解答
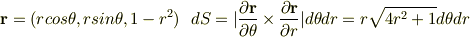
と表せるので,
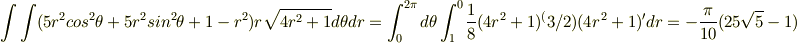
1,自分では面積素の変換は,曲面をxy平面に射影したときのズレみたいのを修正して,二重積分に持って行くための行為と理解しているのですが,この場合はどのような行為を行っているのか自分でもわかりません. 2,答えはマイナスがなかったのですが,どこで間違えてしまったのかわからないのでご指摘お願いします.
Re: 面積分の問題
山本明 さんのレス (2005/07/10(Sun) 10:03)
1.
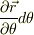 というのは,θという変数をわずかにずらしたときに位置ベクトルがどれだけ変化しているかを表すベクトル.そして
というのは,θという変数をわずかにずらしたときに位置ベクトルがどれだけ変化しているかを表すベクトル.そして 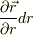 は,変数
は,変数  をわずかにずらしたときに位置ベクトルがどれだけ変化するかを表すベクトルです.
その2つのベクトルの外積の絶対値を計算しているということは,その2つのベクトルが張る平行四辺形の面積を求めているということですね.
をわずかにずらしたときに位置ベクトルがどれだけ変化するかを表すベクトルです.
その2つのベクトルの外積の絶対値を計算しているということは,その2つのベクトルが張る平行四辺形の面積を求めているということですね.
微小面積を考えたいってとき,例えば 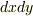 という風に考えることもできます.これって
という風に考えることもできます.これって  をわずかにずらしたときの差を
をわずかにずらしたときの差を 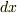 として,
として,  もわずかにずらした差を
もわずかにずらした差を 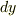 としたときに作られる長方形の面積になっています.いまは
としたときに作られる長方形の面積になっています.いまは 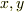 という変数の代わりに,
という変数の代わりに, 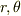 で考えているということです.
で考えているということです.
2.
計算をちゃんと追っていないのですが,  の積分範囲って,0から1なんじゃないですか?
の積分範囲って,0から1なんじゃないですか?
Re: 面積分の問題
Κ さんのレス (2005/07/10(Sun) 12:27)
1,について,ではこの場合は円錐の微小側面積ということで良いのでしょうか?積分範囲はxy平面に射影された領域なんですけど,微小な平行四辺形の場合は射影されたときのズレ(cosα分)は無視できるのでしょうか? 2,z:0→1なんでr:1→0だと思ったのですが.(z=1−r^2より)
Re: 面積分の問題
yama さんのレス (2005/07/10(Sun) 16:23)
まず,面Sは円錐面ではなく回転放物面です. S上の微小領域dSの法線がZ軸となす角をαとします. dSをXY平面に射影したものがrdθdrになるようにdSをとると cosαdS=rdθdr だから dS=(1/cosα)rdθdr となります.cosα分はきちんと計算に含まれているわけです. 当然1/cosα=√(1+4r^2)です. これは,図形的に考えてもわかるでしょう. 積分はθとrについて行うのであって,zについて行うわけではありません. 従ってrの積分範囲は0→1です.
Re: 面積分の問題
Κ さんのレス (2005/07/10(Sun) 16:57)
1,機械的な計算をすることで図形的に考えなくても済むんですね.でもなぜ微小面積(ベクトルの外積で出したやつ)の数字部分が1/cosαに一致するのでしょうか?2つのベクトルが張る平行四辺形の面積を求めただけで,射影したという意識はないのに・・.なんか出来すぎてて不思議です. 2,rはなぜz軸の方向に積分しなければならないのですか?
Re: 面積分の問題
yama さんのレス (2005/07/10(Sun) 18:21)
1 2つのベクトルが張る平行四辺形をXY平面に射影した面積がrdθdrです. 積分の計算に必要なのは,射影した面積ではなく,もとの平行四辺形の面積です. 図形的にcosαを求めて dS=(1/cosα)rdθdr によって平行四辺形の面積を求めなくても,外積の計算で平行四辺形の面積が求まればそれでいいというわけです. 外積の計算には当然Z成分(この場合はd(1-r^2))も含まれますが,z成分を含めることによって自動的にcosαを考慮していることになります.
2 rの積分方向はXY平面上で原点から遠ざかる向きです.Z軸方向ではありません.
Re: 面積分の問題
Κ さんのレス (2005/07/10(Sun) 18:44)
何度もすみません.なんか不思議で.昔の人がこうやると計算できるって発見したってことですかね. >z成分を含めることによって自動的にcosαを考慮していることになります. ここの部分がよくわからないです. あと2なんですがそれは積分の定義ですか?
Re: 面積分の問題
yama さんのレス (2005/07/10(Sun) 21:09)
z成分が0のベクトルすなわちXY平面上のベクトルどうしの外積は,z成分だけを持つベクトルになります. z成分があると外積は(x,y)成分も持つようになり,その結果,(z成分はもとのままで)Z軸と角度αをなす方向に向きます. つまり外積を考えるということは,外積の方向を通じてcosαが関係してくることになるわけです.
∫ydx はX軸方向の積分であってY軸方向の積分ではありません. 同様に ∫(・・・・)dr はr方向の積分です.
Re: 面積分の問題
Κ さんのレス (2005/07/10(Sun) 21:41)
改めて思いましたがベクトルってすごいですね.まだ僕の頭のレベルを遥かにこえているのですが,とりあえず納得できました.ありがとうございました.