曲面の面積

曲面の面積

Κ さんの書込 (2005/07/08(Fri) 17:23)

質問です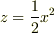． z=\frac{1}{2}x^2 で表される曲面の面積を求めよ．ただし，０≦ｘ≦１，ｙ≦ｘである． > ! Argument of \align* has an extra }. > ...\sqrt{1+x^2}dy=\int _{0}^{1}\sqrt{1+x^2}dx} とやって，ｘ＝sinhθとおき，解いたのですが，そうすると答えにログがでてくるのですが，解答は分数でした．どこが間違っているかわからないので教えてください．お願いします．

Re: 曲面の面積

Κ さんのレス (2005/07/08(Fri) 17:38)

すみません．失敗してしまいました．数式は

\int dS=\int \int \sqrt{1+(\frac{\partial z}{\partial x})+(\frac{\partial z}{\partial y})}dxdy =\int _{0}^{1}dx\int _{0}^{1}\sqrt{1+x^2}dy=\int _{0}^{1} \sqrt{1+x^2} dx

です．

Re: 曲面の面積

yama さんのレス (2005/07/08(Fri) 22:08)

yについての積分範囲が間違っています． その式だと区間[0,1]で積分していることになりますが，区間[0,x]で積分しないといけません． （問題ではｙ≦ｘとなっていますが，これはたぶん0≦ｙ≦ｘということだと思います．）

Re: 曲面の面積

Κ さんのレス (2005/07/08(Fri) 22:54)

本当ですね．しょうもない間違いですみません．ありがとうございました．