無題

ハテナさんの書込 (2005/07/08(Fri) 14:08)

どうしても考えても分からない問題があります．分かる方お願いいたします．地上から弾を打ち出して前方Ａの地点の真上Ｂの高さに置かれた的に命中させるには，最低でどれだけの初速を必要とするか？またそのとき，打ち出すべき角度はどうか？風などの影響は一切ないものとする．

Re: 無題

FKD さんのレス (2005/07/08(Fri) 19:12)

ハテナさんこんにちは

力学の問題のようですが，高校生か大学生の方でしょうか？

とりあえず，適当に座標を設定し，弾の運動方程式を立ててみると見通しが立つと思います．

Re: 無題

ken さんのレス (2005/07/09(Sat) 14:52)

kenです．

ハテナさんFKDさんこんにちは

この問題，高校生でも解けるだろうけど，難しいとおもいますよ．

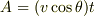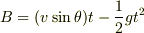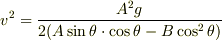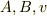速さを ,水平面に対する角度を $\theta$ とすると水平方向x側は $A=(v \cos \theta )t$ 垂直方向y側は $B=(v \sin \theta )t-\frac{1}{2}gt^2$ となり，これを解くと $v^2=\frac{A^2g}{2(A \sin \theta \cdot \cos \theta - B \cos ^2 \theta)}$ となります．ここまではハテナさんは理解できていますか？ここから A,B,v がすべて実数であり，vが最小となる 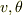$v,\theta$ を求めるのは簡単にはいきません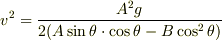． $v^2=\frac{A^2g}{2(A \sin \theta \cdot \cos \theta - B \cos ^2 \theta)}$ を $\theta$ で微分して極小値を求めればいいでしょうか？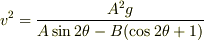その方法でも解けるかもしれませんが，挫折する可能性が高いでしょう．なお，ハテナさんがここまで自力で持ってこれるのであれば，テストはもちろんこの掲示板でも，書いておくほうが望ましいでしょう．さて，上の式を変形して $v^2=\frac{A^2g}{A \sin 2\theta - B( \cos 2 \theta +1)}$ としたら見やすくなったでしょうか．

http://www12.plala.or.jp/ksp/mathInPhys/trifuncCombine/index.html

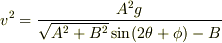を参考にして $v^2=\frac{A^2g}{\sqrt{A^2+B^2} \sin (2\theta + \phi)-B}$ と変形するとよりわかりやすいでしょう．

Re: 無題

ハテナさんのレス (2005/07/09(Sat) 23:53)

みなさんありがとうございます．θで微分する以外に全く考えつきませんでした．変形すると考えやすそうです．あと少しがんばってみます．

[home] [掲示板] [ページの先頭]