るい さんの書込 (2005/07/04(Mon) 06:56)

粒子の散乱の問題で，

?『半径aの絶対球(剛体球)の散乱断面積を求めよ．剛体球のポテンシャルは，ｒ＜aでU＝∞，ｒ 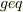aでU＝０であるものとする』

この解答の中で，微分散乱断面積ｄσと立体角oの関係式，ｄσ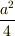＝ doを求めたのですが，この式は物理的になにを表しているのですか？

?『ｄσ＝２πρｄρを使い，[χ，π]の区間に散乱される粒子の散乱断面積を求めよ』

この解答の中で， σ(χ，π)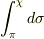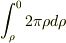＝ ＝ という積分が書いてあったのですが，この積分範囲はどうやって考えて変換しているのですか？

??の解答中の式をとりあえず実行してみたら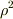， ＝− となりました． マイナスの散乱断面積というのは解答としてあっているのですか？ この散乱断面積は，物理的になにを意味しているのでしょうか？

以上の３つを教えてください．

yama さんのレス (2005/07/04(Mon) 21:28)

散乱断面積の物理的意味については，言葉だけの説明では分かりにくいと思います． 大抵の力学の教科書には図を用いた説明がのっていると思うので，まず教科書をよく読んでください． dσとdoの関係は一般には散乱角にも関係しますが，剛体球の場合には散乱角に関係しないということを導かれた式は意味しています． つまり，あらゆる方向に均等に散乱されるわけです． ?の解答の式にはちょっと疑問点があります． [χ，π]の区間というのは散乱角θがχからπまでということだと思います． そうすると積分範囲ははθ=χからθ=πまでになります． また散乱断面積は，最終的にはχを含む式で表すべきでしょう． 面積としては普通は負の値は考えないので，絶対値をとるべきでしょう．

isuzu さんのレス (2005/07/07(Thu) 13:04)

遅くなってしまって，すみません． 答えてくださってありがとうございます．

自分でもいろいろ考えてみました．

ｄσ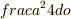＝ については， 「立体角が触れ角に依存しないので，散乱は等方的であることを表している」． σ= πρ^2については， 「散乱されるために通らなければならない面積は，半径ρの球の断面積である」．

というふうに考えました．

これはあっていますか?

ｙama さんのレス (2005/07/07(Thu) 17:29)

合っていると思いますが，ρをχで表すか，または何らかの説明をつけておく必要はないでしょうか． さらに，この場合は半径aの球を考えているので「半径ρの球の断面積」というのは間違いではないにしても奇妙な感じがします． 「半径ρの円の面積」としたほうがよいと思います.