自然単位系で

id さんの書込 (2005/07/01(Fri) 09:19)

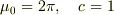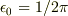自然単位系では $\mu_0 = 2 \pi, \quad c = 1$ とするそうですが，そうなると $\epsilon_0 = 1/2\pi$ になりますよね．

つまり自然単位系で，たとえば電磁場のエネルギー密度は

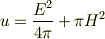
$u = \frac{E^2}{4\pi}+\pi H^2$

という形になり，自分には何とも不愉快に見えます．

しかしハナっから 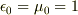$\epsilon_0 = \mu_0 = 1$ としてしまえば，少なくとも自分の思いついた数式においては E-H対応，E-B対応共に，美しい形にそろってくれるようでした．

それなのに何故 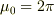$\mu_0 = 2\pi$ という定義の仕方をするんでしょうか?

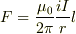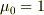$F = \frac{\mu_0}{2\pi} \frac{iI}{r} l$ で電流を定義する際に，「 $\mu_0 = 1$ で係数を無理数にすると，電流を定義しにくいから」などという安直な理由ではないとは思うのですが・・・