msndance さんの書込 (2005/06/30(Thu) 11:24)

以前，gooで質問をしたことがあるのですが，未解決のまま締め切ってしまいました． あれから１ヶ月ほど考えたんですが，どうしてもわからないので， こちらに投稿してみます．わかる方いましたらお返事お願いいたします．

太陽の銀河系の中心からの距離:a[m] 太陽のそのまわりの公転周期:P(秒) 銀河系の質量:M[kg] 太陽の質量<<銀河系の質量 だから， a^3/P^2=GM/4π^2 ここでaを天文単位，Pを年単位，銀河系の質量を太陽の質量の倍数で表せば，G/4π^2=1………(*)となるから，常識はa^3/P^2=M したがって，求める質量Mは上式のaに3*10^4光年=1,9*10^9天文単位，Pに2.2*10^8年を代入して M=(1.9*10^9)^3/(2.2*10^8)^2=1.4*10^11(倍)

(*)の式なんですが，どうして単純に1になるんでしょうか？

ｙama さんのレス (2005/06/30(Thu) 12:32)

地球の公転半径をr，公転周期をT，太陽の質量をmとすると Gm/4π^2=r^3/T^2 となりますが，r＝1（天文単位），T＝1（年），m＝1（太陽質量）を代入すると G/4π^2=1 になります． 右辺の1には「天文単位^3/太陽質量・年^2」という単位がついていると考えたほうがいいでしょう．

msndance さんのレス (2005/07/02(Sat) 14:52)

>m＝1（太陽質量）を代入すると

あ〜〜〜〜，なるほど，これは思いつかなかったです． このように単位指定したから成り立つ式なんですね

CO さんのレス (2005/07/03(Sun) 02:41)

余談になりますが，天文学では質量を太陽質量の何倍かで表すことが多いです．太陽質量を 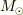で表します． :)

Joh さんのレス (2005/07/03(Sun) 04:23)

odot なんて記号知りませんでした！ :)

CO さんのレス (2005/07/03(Sun) 12:19)

Joh さん > odot なんて記号知りませんでした！ :)

あまり使われない記号なので，tex 以外で書くときにどうしたら良いものか迷います :(