近似
近似
isuzu さんの書込 (2005/06/29(Wed) 20:06)
単振り子（鉛直と糸との角度θ，質量ｍ）において，T＝const for Eとなるのはポテンシャル（地面を基準として）Uが，U＝ｍｇ(１−cosθ）＝ｍｇ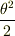 
となるときなのだと講義でやったのですが，いまいちわかりません．
Uがどういうときに，TがEに関してconstではなくなるのですか？ あと，cosθの近似で，二乗項までとるのには，なにか物理的な意味があるのですか？ふつうに高次の微小量だから，とかんがえてよいのですか？ その場合，なぜ，cosθ＝１と近似せず，二乗項までを必要とするのですか？
教えてください．
Re: 近似
yama さんのレス (2005/06/29(Wed) 22:36)
cosθ＝１の近似ではポテンシャルが定数になってしまうので力がはたらきません． 2次の項までとると，θに比例する復元力がはたらくので線形振動となり周期が一定になります． 4次以上の項までとると，非線形振動になり周期は振幅に関係します． つまり２次の項までで近似できるときに周期が一定になるわけです．
Re: 近似
isuzu さんのレス (2005/06/30(Thu) 19:53)
yamaさん，返信ありがとうございます． 線形振動・非線形振動，というのを初めて聞きました． どう区別しているのですか？ 非線形振動で周期が振幅の関数になるというのは，どうやたら導けるのですか？
Re: 近似
Re: 近似
yama さんのレス (2005/07/01(Fri) 00:04)
線形振動の運動方程式は線形微分方程式で，非線形振動の運動方程式は非線形微分方程式です． 線形振動では，ばね振子のように，平衡点からの変位に比例する復元力がはたらき，その結果振幅に関係なく周期が一定になります． 非線形振動では，単振子のように，復元力は変位に比例しません．その場合，一般に周期は振幅によって変わります．微小振動の場合は近似的に線形振動と見なせます．
Re: 近似
isuzu さんのレス (2005/07/03(Sun) 15:20)
yamaさんがおっしゃることは，理解できました．ありがとうございました．
COさんが紹介してくださったページも読んだのですが， 結果の周期Tで二次以上の項は無視して，一次の項のみをとるとき周期一定となるのは，積分後だからですか？
Re: 近似
yama さんのレス (2005/07/03(Sun) 18:31)
積分前でも，ポテンシャルでθの1次までとるか，運動方程式でθの1次までとるかで違いが出ます． cosθをθの級数に展開すると1次の項がないので，ポテンシャルで1次の項までとると結局cosθ=1となって，力がはたらきません． ２次の項までとれば，運動方程式にはθの1次の項しか現れないので周期は一定になります． ポテンシャルのcosθをそのままにして，運動方程式を導くとsinθが現れますが，1次の項までとってsinθ=θと置くと周期は一定になります．
