Κ さんの書込 (2005/06/29(Wed) 17:53)

こんにちは．この掲示板は同じ人が同時に二つの記事を作ることは禁止されているのでしょうか？もしそうならこちらは削除してください． 面積分についてなのですが 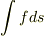のとき，ｆやＳをなんの量をとるかで意味がかわってきますよね？例えばｆを面密度とすれば，面全体の質量となるし，ｆをｆ（u,v)という関数ととれば面と，面をxy平面に射影した部分の間の体積になりますよね？ベクトルの面積分なんてのもあるみたいですし．そもそも積分は単にインテグラル以降の微小量を集めたものであるから，面積分なんて特別な名前をつける意味はあるのだろうか？ 面積分の具体的な定義は何なのですか？様々な参考書を調べたのですが，上の例のいずれか一つをあげて「このような計算を面積分という」としか書かれておらず具体的にはわかりません．あと物理のどのような分野で役立つのかも教えてほしいです．

FKD さんのレス (2005/06/29(Wed) 18:37)

積分 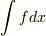において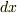， が微小長さなのが線積分， 微小面積なのが面積分，微小体積なのが体積積分であったと記憶しています． 面積分が役立つ物理の分野ですが， 有名どころでは電磁気学のガウスの法則の積分型などでしょうか．

• http://www12.plala.or.jp/ksp/formula/physFormula/html/node50.html

Joh さんのレス (2005/06/29(Wed) 18:54)

微分形式という理論を勉強すると，すっきり分かるのですが，E3空間では，一次微分形式が線積分，二次微分形式が面積分，三次微分形式が体積分となります．関数そのものは零次微分形式，四次以降の微分形式は零です．一般にn次元ベクトル空間で，n次微分形式まで定義できます．ちょっと，自分で調べてみてください．

Κ さんのレス (2005/07/01(Fri) 15:26)

お二人ともありがとうございます．微分形式について調べたのですが，少し難解なので時間をかけて勉強してみます． ちょっと本題とはずれるのですが，面積素を書き換えるとき 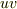というパラメータがでてきますよね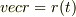？ におけるｔが時間とみなせるように，何か物理的な具体例はないでしょうか？なぜ急に２つのパラメータを導入したのかわかりません．

Κ さんのレス (2005/07/01(Fri) 15:28)

→ に訂正です．

やかん さんのレス (2005/07/01(Fri) 16:34)

＞面積分なんて特別な名前をつける意味はあるのだろうか？

昔，砂川重信先生の電磁気学入門を読んだ時に， 線積分，面積分といっても実際にかけるのは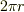， だったり 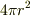だったり，計算はいたって簡単な事が多い，と書いてありましたが，線や面がぐにゃぐにゃ，でこぼこでも通用するような一般化した”表記方法”，という事で意味があるからなのでしょうか．

＞様々な参考書を調べたのですが，上の例のいずれか一つをあげて「このような計算を面積分という」としか書かれておらず具体的にはわかりません．

定義としては本に書いてある通りなんでしょうけど，外積でも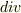， でもいきなり定義式だけ書かれると，無味乾燥ですよね．私がこちらで御紹介いただいた”道具としての物理数学”

• http://www.amazon.co.jp/exec/obidos/ASIN/4534034903/249-9188129-0579522

という本は，そういう点に義憤を感じ，書かれているようでわかりやすかったです（でも最後の方は”こうなるのだけは認めてっ，”て感じで難しかったなあ）．２番目のご質問は私ごときではわからずすみません・・・．

ｙama さんのレス (2005/07/01(Fri) 18:03)

面は2次元の広がりを持つので，その面を覆うには２つのパラメータが必要になります． パラメーターが１つだけのとき，そのパラメータの値を変化させればパラメータによって指定される点は曲線上を動きます．しかし１つの曲線では面を覆うことはできません． パラメータを２つにすると，そのうちの1つを固定してもう一方を変化させると1つの曲線が描かれます．さらにもう１つのパラメータを連続的に変化させるとその曲線が空間を動いて曲面を描きます． 物理的な具体例はあまり思いつきませんがつぎのような例はどうでしょうか． 地球上の位置を表すとき緯度や経度を座標と考えることができますが，一方，地球中心を原点とするデカルト座標（x,y,z）で地球上の位置を表すこともできます． この場合，緯度や経度を指定すれば（x,y,z）が定まるので，緯度や経度を（x,y,z）を定めるパラメータとみなすこともできます．

Κ さんのレス (2005/07/01(Fri) 20:06)

＞やかんさん ありがとうございます．その本は読んだことがあります．似たような本ももっていて確かに解りやすく，物理にも応用しやすいのですが深いところまで乗っていないのが難点ですね． ＞yamaさん かなり解りやすい例ありがとうございます．緯度，経度がu,vってことですよね．そこで，関係性はわかったのですがなぜu,vというパラメータを導入したのでしょうか？今まではずっと（x,y,z)自体を変化させていたのに．

Joh さんのレス (2005/07/01(Fri) 21:38)

面は二次元だから，パラメーターは二つでいいんじゃないでしょうか．

yama さんのレス (2005/07/02(Sat) 17:37)

(x,y,z)で曲面上の位置を表す場合，曲面の方程式f(x,y,z)=0が満たされる必要があります．(x,y,z)の値に制限が無ければ３次元に広がってしまうので，条件をつけて２次元にしているわけです． これに対してパラメータ(u,v)を用いて表す場合，(u,v)を曲面上の座標とみなすことができます．この曲面上の座標を用いて，曲面上の距離，面積，ガウス曲率などを表すことができますが，２次元のものを２つの変数で表すのは自然なことだと思います．

Κ さんのレス (2005/07/02(Sat) 22:02)

高校のときから使っている直交座標とは違うということでしょうか？でもu,v によってx,y,zが決まるのだから同じことではないのですか？

yama さんのレス (2005/07/03(Sun) 00:06)

もちろん内容的には同じことですが，同じことを表すにもいろいろな表現方法があります． (x,y,z)を用いるのと(u,v)を用いるのとは表現方法の違いです． 半径aの球面上の位置を(x,y,z)で表す場合，(x,y,z)にでたらめな値を与えたのでは球面上の点にはなりません． x^2+y^2+z^2=a^2 を満たす(x,y,z)だけが球面上の点になります． これに対して(u,v)をパラメータとして x=a sin u cos v y=a sin u sin v z=a cos u と置くと x^2+y^2+z^2=a^2 が自動的に満たされるため任意の(u,v)が球面上の点に対応します． そのため任意の(u,v)を球面上の座標と考えることができます． （ただし1対１対応のためには0≦u≦π，0≦v＜2πのような制限が必要ですが） 幾何学的にはuを天頂角，vを方位角と考えることができます．

どちらの表し方がよいかは，問題によって違うと思いますが，たとえば球面上の積分を計算するときは(u,v)を用いたほうが計算が簡単になると思います．

Κ さんのレス (2005/07/03(Sun) 01:01)

問題の簡単のために導入したって感じでしょうか？なんとなくわかってきました． 変な質問なのですがx^2+y^2+z^2=a^2とかx=a sin u cos v，y=a sin u sin v， z=a cos uが球面を表すというのはなぜ知っているのですか？暗記ですか？ もちろん僕も問題とかで見かけているのでなんとなくはわかるのですが，空間と方程式の関係は，高校でもしっかりやっていないし（そんな分野はなかった），大学では知ってる前提でやっているみたいな感じなので．

Joh さんのレス (2005/07/03(Sun) 04:34)

私も最初はどっかで習ったことですが，一度納得しておけば，忘れてしまっても自分で導けるようになります．丸暗記はいけません．高校で習うことと，大学で知っていると前提にされていることの間には，少しギャップがあるかもしれませんが，そこで自分で勉強して埋めるしかないでしょう．

平面上で，円を 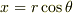, 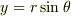って表せるのは知ってますか？もし知ってたら，球の絵を描いて，もうひと工夫加えれば，球のパラメーター表示も導けると思います．練習問題だと思ってやってみてください．

Κ さんのレス (2005/07/03(Sun) 23:44)

P(x,y,z)としてpからz軸におろした点をA，xy面に降ろした点をBとすると，ＯＢ＝asinu，PB=acosuで，ｘ＝OBcosv,y=PBsinv,z=PBに代入，であってますよね． なんかＸＹＺからパラメータにするのって難しいですね．図形的にやらなきゃだめっていうか．

yama さんのレス (2005/07/04(Mon) 23:05)

図形的に考えればそうなりますね． また，次のように形式的に導くこともできます． x^2+y^2+z^2=a^2で x^2+y^2=ρ^2・・・・? と置くと ρ^2+z^2=a^2・・・・? となりますが，?は x=ρ cos v，y=ρ sin v ?は ｚ=a cos u，ρ=a sin u と置けるので，これからパラメータ表示が導けます． この方法は図形的な意味がわかりにくいのが欠点ですが，同じような方法で4次元超球面 w^2+x^2+y^2+z^2=a^2 を３個のパラメータで表す式も簡単に導けます．

Κ さんのレス (2005/07/04(Mon) 23:25)

すみません．?式はどこからでてきたのですか？

yama さんのレス (2005/07/04(Mon) 23:38)

(x^2+y^2)+z^2=a^2 で x^2+y^2 を ρ^2 で置き換えれば?式になります．

Κ さんのレス (2005/07/05(Tue) 01:59)

なるほど．便利ですね．自分でも曲面についての本を見つけたので勉強してみます． 勉強になりました．皆さんありがとうございました．