佳祐　高専５年 さんの書込 (2005/06/29(Wed) 01:04)

はじめまして．今年編入学試験を受ける高専５年生です．さっそく質問よろしいでしょうか？

電場を計算する場合，ガウスの法則

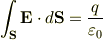
を使うと，たとえば，内径 a，外径 b の中空導体球（荷電していない）の中心に，電荷 Q をおくとき，球の内部の，その中心から距離 r における電場は，ガウスの法則から，

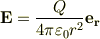
となりますよね．このとき，電荷 Q によって，中空球内面に，負の電荷が誘導されていますが，これは電場を計算する際には，計算に含みません．

そこで，平行平板コンデンサ（面積 A，幅 d）を考えると，これが両極それぞれ +Q，-Q で帯電していたとして，この +Q に帯電した極板の周りに閉曲面を考えると，この閉曲面を極板に限りなく近づけたとき，ガウスの法則から

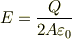
となるはずです．ところが，実際に極板間に生じる電場は

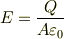
が正しいはずです．これって矛盾してないのでしょうか？

先生に聞いてみたところ， 「もう一つの極板から，

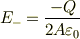
という電場があるから，これにより極板間の電場は 2 倍になり，外側の電場は打ち消して 0 になる」 という説明があって，一度は納得したのですが，それだと最初の例で考えた 「電場を計算する際は，閉曲面外の電荷による電場は計算に含まない」 というところが引っかかって，やっぱり理解できません．どのように，理解すればよいのでしょうか？平行平板コンデンサの場合だけ，パターンとして覚えてもいいのですが…

かなり低レベルな質問だと思いますが，解説宜しくお願いします．

山本明 さんのレス (2005/06/29(Wed) 02:19)

はじめまして．

簡単にヒントだけ． 極板間の電場は，それぞれの極板が作る電場を足し算する――って方針は，どちらの場合も同じです． 平行平板コンデンサーの場合，どちらの極板も極板間に電場を作りますね． それに対して，球状に電荷が分布しているときは，分布している半径より大きい場所には電場を発生させるけど，分布している半径より小さい場所には電場を発生させませんね．とすると，極板間の電場は，内側の極板が作る電場＋外側の極板が作る電場となり・・・． ヒントは以上．

編入試験，がんばってください :)

toorisugari no Hiro さんのレス (2005/06/29(Wed) 03:29)

> 「電場を計算する際は，閉曲面外の電荷による電場は計算に含まない」 > というところが引っかかって，やっぱり理解できません．

積分計算をしてみれば明らかなのですが，実際に， 球内面の各点から中空内の一点にかかる電場ベクトルを図で書いてみれば 足しあわせたときどうなるか予想ができると思います．

ｙama さんのレス (2005/06/29(Wed) 09:21)

>「電場を計算する際は，閉曲面外の電荷による電場は計算に含まない」

これは間違いです．「電束を計算する際は・・・・」とすれば正しいのですが． 電束は電場を閉曲面上で積分したものですが，閉曲面外の電荷はこの積分値に関係しないということです． 外部電荷による電場は閉曲面内部にも侵入します．しかし，積分すれば０になります． たとえば閉曲面内部に電荷が無い場合，外部から内部に入ってきた電気力線は再び外部に出て行くので積分値には影響しないわけです． コンデンサの例では，1枚の極版だけがあって外部に向かって両側に強さEの電場を生じている場合，極版を囲む閉曲面上の積分値は2εEAです． 近くに逆符号の電荷をもつもう1枚の極版がある場合，極版の片側の電場は2E，反対側の電場は０になりますが，極版を囲む閉曲面上で積分するとやはり2εEAになります．

なお，点電荷を中心とする中空導体球がある場合,内部の電場は導体球が無い場合と同じになりますが，点電荷が中心からずれると，電場は導体球が無い場合とは異なってきます． これは電気力線を描いてみればわかるでしょう．電気力線は導体球内面に垂直になるからです．しかし，点電荷の周りの閉曲面上の積分値は変わりません．

なお，導体球の外部の電荷は内部には影響しませんが，これは導体による静電遮蔽なので，ガウスの定理と混同しないように．

佳祐　高専５年 さんのレス (2005/06/29(Wed) 23:58)

返信ありがとうございます！ガウスの法則で電場を計算する際は，閉曲面の外側の電荷を考えないと思っていました…違ってたんですね．知らなかったです． もう少し，調べて考えて見ます．また分からなかったら質問するかもしれませんが，そのときはまたお願いします．

toorisugari no Hiro さんのレス (2005/06/30(Thu) 17:38)

> ガウスの法則で電場を計算する際は，閉曲面の外側の電荷を考えないと > 思っていました…違ってたんですね．

いえ，考える必要はありません．

ただこれは閉曲面を通過する電束（電気力線の本数）の値，言い換えれば 各点の電場（正確には電束密度）ベクトルの法線成分(×面積)の「合計」に 影響しないといってるだけで，「各点の電場」は閉曲面の外側の電荷 の影響を受けます．(閉曲面全体で総和すると打ち消しあって，影響が消えますが)．

今回の問題は外側の電荷分布が球対称である特別な場合であり，このときは 「合計」だけでなく「各点」の電場も0になるということです．

ガウスの法則と対称性を組み合わせると各点の電場(電束密度）が簡単に 計算できますが，これはどの教科書にも載っている事項なので調べてみ てください．

yama さんのレス (2005/06/30(Thu) 23:42)

ガウスの定理を適用する場合は，電束を表す表面積分を閉曲面内の全電荷に等しいと置きます． 当然，外部電荷は閉曲面内の電荷には含まれないので，式の中に外部電荷が直接入ってくることはありません． だったら外部電荷は無いものと考えて電場を求めればいいかというと，そうでもありません． 外部電荷の影響によって表面積分を表す式の具体的な形が違ってくるからです． たとえば帯電した1枚の極板だけがある場合は電場は両側に対称的に生じるので，電束を表す積分は2εEAになります． それに対して，逆に帯電した極板が近くにある場合は，片側にだけ電場を生じ，反対側の電場は０になるので，電束を表す表面積分はεEA＋ε・0・Aになります． どちらの場合も，それを極板の全電荷Qに等しいと置きますが，その結果，前者ではE＝Q/2εA（両側）が得られ，後者ではE＝Q/εA（片側だけ）が得られます． 点電荷を中心とする中空導体球がある場合は，内部の電場の球対称性は，導体球が無い場合と変わらず，従って電束を表す面積分の式の形も変わりません． 従って，この場合の電場は導体球が無い場合と同じになります． しかし，点電荷が中心からずれると，電場は球対称でなくなるので，電束を表す式の具体的な形は，導体球が無い場合とは違ってきます．当然，電場も導体球が無い場合とは違ってきますが，ガウスの定理を用いて電場を求めるのは困難です． 一般に電場の対称性が低い場合はガウスの定理で電場を求めるのは難しく，他の方法を用いないといけません．たとえば導体球の場合は鏡像法を使うことができます．

佳祐　高専５年 さんのレス (2005/07/01(Fri) 20:52)

電束密度や，電気力線は授業でやらなかった内容なので，教科書（岩波書店物理入門コース）を読み直してみました．電場の求め方もかなり理解できたと思います．丁寧な解説を，みなさんありがとうございます．