量子力学で・・・

id さんの書込 (2005/06/24(Fri) 11:10)

はじめまして．常々拝見させていただいております．量子力学の序盤でつまずいてしまい，気持ちが前に進めません(泣突然なのですが質問させてください．

ネタは (位相速度)=(粒子の速度)/2 となってしまうことについてです．

電子など，波動性を持つ粒子では

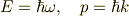
$E = \hbar \omega, \quad p = \hbar k$

が成り立つと言われている・・と思います．そこに粒子の速度をとすれば，粒子性として

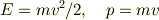
$E = mv^2/2, \quad p = mv$

も成り立つと言われている・・と思います．そして波動性として，位相速度を 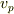v_p とし

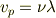
$v_p = \nu \lambda$

も成り立つと思います．

で，上式達をいじくると， (位相速度)=(粒子の速度)/2 という関係が得られてしまうのは有名な話だと思います． (群速度)=(粒子の速度) となってはくれますが・・・

これをもって，「速度よりも運動量の方が基本的な量である」と，砂川さんの著書「量子力学の考え方」に書かれていたと記憶しています．

「速度よりも運動量の方が基本的な量である」というのは納得できるのですが，何にしろ (位相速度)=(粒子の速度)/2 という関係が得られてしまうことに変わりありません．これはどう解釈すれば良いのでしょうか?

自分なりに考えてみたところ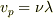， $v_p = \nu \lambda$ は実在波のみに成り立つ関係なのかな? などと思ったりしたのですが，当然そんなこともないようで・・・どうにも解決できません．

どうか助言おねがいします．

最大値の点での位相速度は，古典的な粒子の速度に一致するようです．

の受け売りです．idさんは疑問をもちながら勉強をしておられるようで，僕も見習わないとと思います :)

ありがとうございます．「振動・波動」の勉強をテキトーに流してきてしまった身なので，式の意味を完全になぞることはできなかったのですが(^^;

つまりは（node5.html の中盤にあるように）

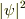$|\psi|^2$ ：粒子の存在確率(?)が最大となる点の移動速度が古典的粒子の速度となり，それに対応するのは群速度である

ということでしょうか？群速度というのは，要するにうなり構造の速度ですよね？

となると，ド・ブロイ波は分散関係：

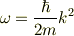
$\omega = \frac{\hbar }{2m} k^2$

を持つので，時間の経過と共に波の形は崩れていく(?)，つまり時間が経つと粒子の存在確率はあやふやになっていく？？（あれ？群速度とは関係ないかな・・・？

こんがらがってしまいました(^^; 初学者が「量子力学」を理解しながら勉強することは難しいですね．「とにかく，そういうもんなんだ」と思いながら勉強していくことにします．

崎間さんありがとうございました．「かぎプロジェクト」応援しています！