ベクトル解析
ベクトル解析
Κ さんの書込 (2005/06/24(Fri) 00:17)
こんばんは.ちょっとした疑問です. |e5a2631b529ff7e4dfed0b651e53b431|r|d9d1fa6b9b087b8420961a1c08d4b57e| という弧長の式があったとき,drとdr/dtは同じ方向なのでしょうか?drは集めると弧長の長さになるので,接線方向の微小ベクトルだと思うのですが,dr/dtはtを0に近づけたから接線方向になったわけで,(つまりdtのおかげで)どちらも同じ方向というのは納得できないです.
Re: ベクトル解析
yama さんのレス (2005/06/24(Fri) 08:13)
drはベクトル,dtはスカラーです. dr/dtはベクトルをスカラーで割ったものだから,もとのベクトルと同じ方向のベクトルです.
Re: ベクトル解析
やかん さんのレス (2005/06/24(Fri) 08:23)
Kさん,yamaさん,はじめまして.
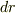 がすでに接線方向を向いていると考えたらどうでしょうか.?
がすでに接線方向を向いていると考えたらどうでしょうか.?  はまだ接線方向を向いてないけれども,
はまだ接線方向を向いてないけれども, 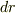 は
は  のおかげでもう向いちゃってるとか・・・.ライプニッツの微分記号は分母子ばらすと微分というし,?と違って
微分される事が前提という事でしょうか・・・(うそかもしれません (^^;)
のおかげでもう向いちゃってるとか・・・.ライプニッツの微分記号は分母子ばらすと微分というし,?と違って
微分される事が前提という事でしょうか・・・(うそかもしれません (^^;)
Re: ベクトル解析
Κ さんのレス (2005/06/25(Sat) 00:31)
返信ありがとうございます.たしかにyamaさんのように考えると納得はできるのですが・・.
>?はまだ接線方向を向いてないけれども, 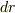 は
は  のおかげでもう向いちゃってるとか・・・.
この部分が疑問で,?r(接線でない)→?r/?t→dr/dt(この時点で接線方向になった)→dr(dtがなくても接線?)みたいな疑問の流れなのですが.
のおかげでもう向いちゃってるとか・・・.
この部分が疑問で,?r(接線でない)→?r/?t→dr/dt(この時点で接線方向になった)→dr(dtがなくても接線?)みたいな疑問の流れなのですが.
Re: ベクトル解析
yama さんのレス (2005/06/25(Sat) 18:06)
drは接線方向の無限小ベクトル,dtは無限小のスカラーだから,dr/dtは有限の大きさをもつ接線方向のベクトルです.
Re: ベクトル解析
やかん さんのレス (2005/06/26(Sun) 13:10)
こう考えていいかどうかわかりませんが,接点は1点ですから,定義できるのはtの変化に対するrの瞬間変化率の方向と大きさのみ,つまりΔt→0とした時の値,方向のみですから,tの関与なく,rの増加分は接線方向を向きませんよね.
>dr(dtがなくても接線?)みたいな疑問の流れなのですが.
やはり,drって,dtあることが前提じゃないかなあ.yamaさんがお書きになったように, dのつく無限小って,大きさないから概念的なもので,接点1点だけでは,drって矢印書くのもあくまで便宜上の事であって(本来目で見えない?),Δr書くのと本質的には違うような気もしますね.
Re: ベクトル解析
Κ さんのレス (2005/06/26(Sun) 14:26)
yamaさんのおっしゃることはわかるのですが,ぼくはやかんさんと同じ考えです.やはり 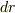 を考えること自体いけないのでしょうか?計算のときだけ形式的にyamaさんのように考えていくというか.
を考えること自体いけないのでしょうか?計算のときだけ形式的にyamaさんのように考えていくというか.
Re: ベクトル解析
yama さんのレス (2005/06/26(Sun) 15:23)
一応その通りですと言っておきましょう. 普通の実数論の枠内では,∫drやdr/dtは意味を持ちますが,dr自体は意味が無く,その方向を考えることはできません. また,?t→0のときの?rの極限値をdrと考えるとしても,それは0ベクトルになるので方向を考えることはできません. さらにdr/dtは?r/?tの極限値であって,drをdtで割ったものではありません. いずれにしても,drの方向というのは意味がありません.
しかし,数学的厳密さはともかく,物理では無限小時間とか無限小変位とかの概念は普通に用いられ,微分係数を無限小どうしの割り算とみなすこともよくあります.この観点ではdrは曲線上の無限小変位であり,また,接線方向の無限小ベクトルであると考えることができます. これは数学的には超準解析(non-standard analysis)の枠内で定式化することができます.超準解析では実数体を拡大し,無限小や無限大も取り込みます. 例えば,すべての(普通の)正の実数より小さい正の数(正の無限小)が存在します. いろいろな無限小が存在し,無限小どうしの演算や大小関係も考えられます. dtやdrも無限小量として意味を持ちます.
Re: ベクトル解析
やかん さんのレス (2005/06/27(Mon) 17:54)
なるほど・・・.超準解析というのですか・・・. 無限小や,無限大がもちゃんと考えられるんですね. とても不思議 :)
Re: ベクトル解析
Κ さんのレス (2005/06/27(Mon) 22:11)
物理的には問題ないということですか.僕は数学があまり得意でないので,いつも数式を物理的意味から入っていくんで疑問に思ったんです.お二人ともありがとうございました. 個人的な興味なんで答えなくてもいいのですけど,yamaさんは数学科の方ですか?
Re: ベクトル解析
yama さんのレス (2005/06/27(Mon) 22:41)
数学科ではなくて物理学科なんですが・・・・それもかなり昔のことで・・・・