グッチ さんの書込 (2005/06/22(Wed) 05:22)

すみません！教えてほしい問題があるのですが・・・

V(x)=Vo{exp(−2x/a)ー2exp(ーx/a)}（ー∞<x<＋∞） なるポテンシャル中に束縛された質量ｍの粒子を考える． （１）ξ=exp(−a/x)とおき，定常状態の粒子の波動関数φ(ξ)の満たすべきシュレーディンガー方程式を導け． （２）このシュレディンガー方程式をξ≒0およびξ>>1の領域でとくと，それぞれ φ∝ξ^λ（λ>0：定数），およびφ∝exp(ーσξ)（σ>0:定数） が得られる．λ，σをm,a,Vo,Eで表せ．

（１）は，普通に {（−(hバー)^2/2m）d^2/(dx)^2φ(ξ)+Vo(ξ^2ーξ)φ(ξ)}＝Eφ(ξ) だと考えたんですが，（２）のほうがわからないんです，φ＝ｋξ^λと仮定して代入していくと，ポテンシャル部分のξ^2ーξが残ってしまってλがでないんです・・・ξ≒０という仮定も使い方がわかりません．どうかわかる方助けてください

山本明 さんのレス (2005/06/23(Thu) 00:17)

ヒントになるかわかりませんが，コメントを付けておきます．

まず(1)．上記のままでもやっていけるでしょうけど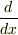， のところに が残っているのが少し気になりました．ここも 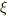で表した方が，わかりやすい式になりそうですね．

また(2)の条件ですが，パッと見た感じ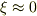では， では 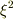を無視して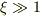， では 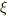を無視する ということかと思いました．だけど 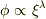と言ってるところを見ると，思い切っ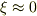て， で 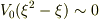としてしまうのかもしれませんね．

…とまあ，そんな感じで続きに挑戦してみてはどうでしょうか． ちなみに上記では「ξ=exp(−a/x)とおき」と書いてあったけど，これは「ξ=exp(−x/a)とおき」の間違いですね??

グッチ さんのレス (2005/06/25(Sat) 05:01)

＞＞山本明さん ちなみに上記では「ξ=exp(−a/x)とおき」と書いてあったけど，これは「ξ=exp(−x/a)とおき」の間違いですね?? >>そのとおりです．すみません d^2/dx^2=ξd/dxξd/dξですよね？ xiapprox 0でV_0(xi^2-xi)sim 0 として代入して計算いくと，それらしい答えになりました．しかし，xiapprox 0ではxi^2を無視して，V=ー2Voξとしてしまうとξの１次の項が残り，λが出ません． ちなみにxigg 1ではxiを無視して，V=Voξ^2としてやってみたのですが，σの方も最後の恒等式が解けません．結局，xiapprox 0でV_0(xi^2-xi)sim 0の場合しか解けませんでした．計算はあってるとおもうのですが・・・どこが違うのでしょうか・・・

グッチ さんのレス (2005/06/25(Sat) 05:05)

すみません，数式コピペしたつもりだったんですが．ξ≒０のときV=0として解いた場合以外 最後のξの恒等式がとけません．ということです．

yama さんのレス (2005/06/25(Sat) 21:23)

ξ≒0のときは，φ＝ξ^λと置いてからξについて最低次の項だけを残し，高次の項を無視する． ξ>>1のときは，φ∝exp(−σξ)と置いてからξについて最高次の項だけを残し，低次の項を無視する． 近似だからこれでいいと思います．

山本明 さんのレス (2005/06/28(Tue) 13:03)

>ξ≒０のときV=0として解いた場合以外最後のξの恒等式がとけません．

ξの恒等式なので，ξのべきごとに両辺の係数が一致する…と考えたらσも決まるんじゃないでしょうか．

>すみません，数式コピペしたつもりだったんですが．

上で書かれた xiapprox 0 といった文字を，＜tex＞と＜/tex＞で囲めば，数式が現れます．← ＜ とか ＞ は半角文字で． 詳しくは，

• http://hooktail.maxwell.jp/yybbs/texuse.html

に書いてありますね．