質問
質問
zak さんの書込 (2005/06/13(Mon) 23:43)
出典：単位が取れる電磁気学ノート 問題：無限に長い導線の中を，定常電流I1が流れている．この導線と同じ平面内に，半径aの円形コイルが，その中心と導線の距離bにおかれている（a<b)．このコイルを以下のような方向に定常電流I2が流れているとき，この円形コイルが導線から受ける力を求めよ．ただし，導線とコイルは真空中にあり真空の誘磁率をμ0とする．
定常電流I1の向き 上向き 定常電流I2の向き 時計まわり
円の中心をO，円形コイルの電流素片の位置をP，半径POのx軸とθの角をなす電流素片I2dsに働く力を考える．電流I1がつくるx>0の領域での磁場の向きは-z方向で，点Pでの磁場の大きさH(θ)は，点Pの電流I1からの距離がb+acosθだから
H(θ)=I1/２π(b+acosθ)となる． よって，点Pにおける電流素片I2dsがこの磁場から受ける力は，I2からH(θ)の方向にねじをひねって，円の接線方向外向きである．また，その大きさをF(θ)dsとすると，
F(θ)ds=μ0H(θ)I2 ds=μ0I1I2ds/2π(b+acosθ) ここまではわかりました． 以下から理解できません．
?具体的な計算は，x方向とy方向に分けて積分しなければいけないが，F(θ)のy成分は，角度θと-θの成分同士が打ち消しあうから，その積分は０である．?また，x成分はθを０から２πまで積分すればよいが，対称性よりθを０からπまで積分し２倍したのと同じである． 以上より，円形コイル全体に働く電流I1による磁場の力Fは， F=∫F(θ)cosθds
?ds=adθだから， F=2∫F(θ)cosθds 積分範囲0→π 以下は計算．
理解できないところ：?に関しては全く理解できません．?に関しては，対称性について理解できませんでした．?に関しても全く理解できませんでした．
よろしくお願いします．
Re: 質問
CO さんのレス (2005/06/14(Tue) 00:33)
こんばんは，zak さん．
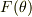の大きさについては分かっているようですが， 
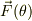が具体的にどの向きをむいていて，その 
成分と 
成分がどのように書けるかはわかりますか？それが分かれば，疑問も解決するのではないかと思います． :)
Re: 質問
zak さんのレス (2005/06/14(Tue) 00:56)
方向はわかるんですが・・・・理解できません，，，．
Re: 質問
CO さんのレス (2005/06/14(Tue) 01:46)
> 点Pにおける電流素片I2dsがこの磁場から受ける力は，I2からH(θ)の方向にねじをひねって，円の接線方向外向きである．
方向はわかる，というのはこれのことでしょうか．これはあってますか？接線方向外向きって・・？
もし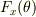 
， 
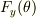が分かっているのならば，それも書いてみてください．
Re: 質問
zak さんのレス (2005/06/14(Tue) 15:42)
すいません．法線方向外向きでした．
Fx(θ)=F(θ)cosθ Fy(θ)=F(θ)sinθ
ですよね？
"F(θ)のy成分は，角度θと-θの成分同士が打ち消しあうから，その積分は０である．" というのはなぜこうなるのでしょうか・・・．
Re: 質問
CO さんのレス (2005/06/14(Tue) 16:40)
> "F(θ)のy成分は，角度θと-θの成分同士が打ち消しあうから，その積分は０である．"
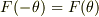です．で，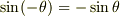 
であるということに注意してください．すると 
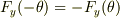です．なので，
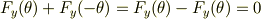
となり打ち消しあっていますよね．
Re: 質問
zak さんのレス (2005/06/14(Tue) 17:50)
すいません，すごく初歩的な質問かもしれないんですが 積分の∫F(θ)sinθdθのθのとこに-θを入れるってことですよね？なぜ-θが出てくるのでしょうか・・・．角度が０から２πまでで-θを使う意味がよくわからないんですが・・．
Re: 質問
CO さんのレス (2005/06/14(Tue) 21:38)
> "F(θ)のy成分は，角度θと-θの成分同士が打ち消しあうから，その積分は０である．"
これを
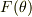「 の 成分は，角度 
と 
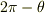の成分同士が打ち消しあうから，その積分は０である．」
と言い換えればわかりますか？
Re: 質問
zak さんのレス (2005/06/15(Wed) 02:49)
難しい〜，，，．でも，やっと理解できました！ありがとうございました．
