積分原理におけるLagrange関数のイメージ

美智代さんの書込 (2005/06/11(Sat) 00:25)

初めて投稿します．物理(系)学科卒の知識レベルです．

物理現象で軌跡を求める考え方として「積分原理」がありますが，例えば光路を求める場合，

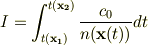
$I=\int_{t(\bf x_1)}^{t(\bf x_2)}\frac{c_0}{n({\bf x}(t))}dt$

という積分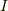が停留値をとる 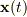${\bf x}(t)$ が求める解ですよね( 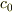c_0 :真空中での光速度， :屈折率)．

この積分原理が表現していることは，「光学的経路長が停留値(まあ最小値ですね)をとる経路が実現される」ということで，被積分関数が意味していることをイメージするのはとても容易です．

これに対して，力学系の場合，

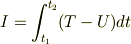
$I=\int_{t_1}^{t_2}(T-U)dt$

という積分を考えるわけですが，こちらは光路の場合と違って，「 T-U の時間積分」が何を意味しているのかが私には直感的にイメージできません．どのようなイメージをもてば，「なるほど，これが停留値をとる経路は確かにちょっと特別な経路だな」と腑に落ちるでしょうか．

こんにちは，美智代さん．

ご質問の件ですが，「物理数学の直感的方法」(長沼伸一郎)の解析力学＠第10章に詳しく書かれています．光学的経路長のような具体的なイメージが得られるかどうかは分かりませんが，読んでみると参考になると思います． :)

ヒントを頂き，どうもありがとうございました．今日，書店で立ち読み(^^;してきました．とても参考になりました．

そうですか，お役に立てて幸いです :)