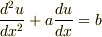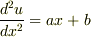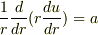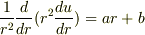教えてください
教えてください
fish さんの書込 (2005/06/09(Thu) 10:10)
はじめまして.工学系の大学をこの春卒業したfishです. 仕事の宿題で以下のような問題が出て,いろいろ調べて自分なりに回答しましたが,恥ずかしながら解けませんでした.是非,教えてください.
In this course, you will need to be able to solve differential equations similar to the following. For each, derive a solution, including constants of integration C1 and C2. in these equations, a and b non-zero constants.
- d2u/dx2 + a du/dx = b
- d2u/dx2 = a x + b
- 1/r d/dr (r du/dr) = a
- 1/r2 d/dr (r2 du/dr) = a r + b
Solve each of these by transforming the equation into a first order differential equation, through a redefinition of the dependent variable. (For instance, for (d), let v= r2 du/dr) Integrate this equation and then transform back into the original variable. Integrate again.
一問目は,両辺をxで積分して du/dx + a u = b x としたのですが,この先,またxで積分しようとすると左辺の2項目にuがあり,どうしたらいいのかわかりません.最初の出だしから間違っているのでしょうか.
二問目は二回,xで積分して u = 1/6 a x3 + 1/2 b x2 としました.これは,検算でuをもう一度二回xで微分すると,問題の式に戻るので,あまり自信がありませんがいいのかなと.C1,C2の定数を使わなければいけないなら,使った場合の解答は, u = 1/6 a x3 + 1/2 b x2 +C1 x + C2 となり,こっちのほうがこの問題にそっているのでしょうか.
三問目・四問目は 問題の例にあるように,左辺の()内をvでおいて計算して,3問めでは 1/r dv/dr = a 両辺にrをかけて dv/dr = a r rで積分して v= 1/2 a r2 vを戻して r du/dr = 1/2 a r2 両辺の1/rをかけてrを消して du/dr = 1/2 a r また,rで積分して u = 1/4 a r2 としました. 四問目も同じ手順で u = 1/12 a r3 + 1/6 b r2 としました.
私の数学の持てる知識を使って解くと上記のようになったのですが,正直間違っている気がかなりします.特に3問目・4問目に関しては,なぜ()にあるrと外のrの扱い方がわからず,上記のようにしてしまいました.是非回答いただけますようよろしくお願いします
Re: 教えてください
Joh さんのレス (2005/06/09(Thu) 11:44)
宿題,お疲れ様です.
あまりまだちゃんと読んでないんですが,2問目は,微分して元の式になったんなら,それでいいんじゃないでしょうか.3問目,4問目は,円筒座標の匂いがプンプンしますね.円筒座標系における,ナブラやラプラシアンを調べてみてください.rの扱いは,それでいいと思います.一問目は,初めから,間違っているようです.ヒントですが, 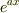 のようなものを,両辺に掛けるとか,そんなの,習ったことないですか?
のようなものを,両辺に掛けるとか,そんなの,習ったことないですか?
ありがとうございます
fish さんのレス (2005/06/09(Thu) 12:07)
ヒントを元に,もう一度解いてみます. ありがとうございました.
もう一度やってみましたが
fish さんのレス (2005/06/09(Thu) 13:44)
一問目の答えは,e*axをかけて,部分積分を使って解くと u =b/a x となりました.
三問目と四問目は円筒座標系で解くということで 調べてみましたが,ラプラシアンの項の中にこの問題の左辺と 似た項があるという共通点は見出せましたが, この問題を積分して解くにあたって,円筒座標と直交座標では どう違うのかがわかりません.
教えてください.
Re: もう一度やってみましたが
toorisugari no Hiro さんのレス (2005/06/09(Thu) 14:29)
(1)は 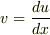 として,式を書き換えてみてください.
見覚えのある式に変わりますよね.変数分離法とかご存じですよね
として,式を書き換えてみてください.
見覚えのある式に変わりますよね.変数分離法とかご存じですよね
(2)は素直に積分するだけ.
(3)(4)は2次元軸対称,3次元球対称のポアッソン問題ですが,
そんな難しいこと考えずに  を右辺に移しながら
順番に積分すれば解けます.
を右辺に移しながら
順番に積分すれば解けます.
見た目はえぐくとも皆素直な問題です.(1)がちょっとむずかしいかな.