質問について
質問について
k.s さんの書込 (2005/06/04(Sat) 17:25)
はじめまして.私は現在工学部で情報科学を専攻しているものです. 物理に興味を持ち,独学で力学を勉強しています. 参考書は,原島著の力学三訂版を使っています. 質問ですが,この本の内容で解らないことがありますが, この掲示板で質問してもよいでしょうか?
Re: 質問について
tomo さんのレス (2005/06/04(Sat) 17:42)
k.sさん,初めまして. tomoです.
> この本の内容で解らないことがありますが, > この掲示板で質問してもよいでしょうか?
大丈夫ですよ :) 質問する時は,「質問をする方へ」を参考にしてくださいね. どの問題(部分)が分からないのか,どのように分からないのか, どこまで分かるのかを書くと,レスがつきやすいと思いますよ.
レスありがとうございます.
k.s さんのレス (2005/06/04(Sat) 21:16)
tomoさん返信ありがとうございます. 早速ですが,質問です.出典は力学三訂版です.よろしくお願いします. 落体の問題で,質点に働く力が,重力の他に速さの2乗に比例する力が作用する場合,速度が以下の式で与えられたとします.
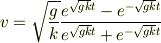
今, 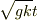 が1に比べて小さくその3次以上の項を省略できるような時間内の速さとtとの関係を求める場合,上のvの式で分子を
が1に比べて小さくその3次以上の項を省略できるような時間内の速さとtとの関係を求める場合,上のvの式で分子を
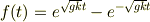
そして分母を
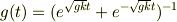
として,それぞれ,tについてマクローリン展開を 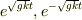 に対して行い,最後に掛け合わせれば,良いのでしょうか?結果は,
に対して行い,最後に掛け合わせれば,良いのでしょうか?結果は,
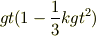
となっていますが,自分で計算した結果は 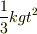 のところが,
のところが, 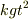 になってしまいます.
どうしたらいよいのでしょうか?
になってしまいます.
どうしたらいよいのでしょうか?
Re: レスありがとうございます.
tomo さんのレス (2005/06/05(Sun) 16:05)
k.sさん,こんにちは.
原島先生の「力学」を見て,実際にマクローリン展開をしてみました.
答えは, 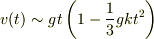 になりました.
簡単に計算の過程を書いておきます.
になりました.
簡単に計算の過程を書いておきます.
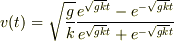
を
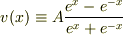
とします( 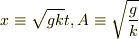 ).
). 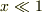 としてマクローリン展開します.
3次まで展開すると,
としてマクローリン展開します.
3次まで展開すると, 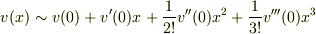 となりますよね.
となりますよね.
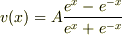 より
より 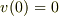
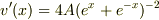 より
より 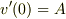
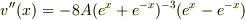 より
より 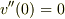
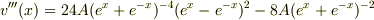 より
より 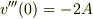
したがって,
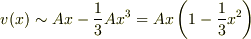
となりますので, 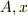 を定義に従って元に戻せば,
を定義に従って元に戻せば,
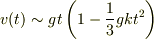
と求まります.
ありがとうございます.
k.s さんのレス (2005/06/05(Sun) 17:03)
tomoさん詳しい解説ありがとうございました.ずっと解らなかった問題が解ってとても,すっきりしました.
ここで,しつこいですがもう一つだけ質問させてください.
問題文のなかで「3次以上の項を省略できるような」とありますが,この意味はマクローリン展開の段階で 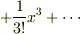 を省略するのではなく,最終的な結果で
を省略するのではなく,最終的な結果で 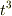 の項がなくなれば良いという意味で良いのでしょうか?
の項がなくなれば良いという意味で良いのでしょうか?
Re: ありがとうございます.
tomo さんのレス (2005/06/05(Sun) 17:23)
k.sさん,こんにちは.
お役に立てたようで,良かったです :)
「3次以上の項を・・・」というところは,私も引っかかりました.今回の答えは,
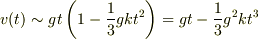 と書けるので,
と書けるので,  の3次の項は無視していないことになります.
この結果を期待するのであれば,問題文では「4次以上の項を無視して」という表現を
使うのが適切ではないかと思います.「3次以上の項を無視して」と言われれば,
2次までを求めるのが普通ですが,結果を見ると3次まで含めていたので,
上の計算には3次まで入れて,その結果に合うようにしたというところです.
この問題の場合,3次を無視すると結果的に1次までになってしまいますしね.
の3次の項は無視していないことになります.
この結果を期待するのであれば,問題文では「4次以上の項を無視して」という表現を
使うのが適切ではないかと思います.「3次以上の項を無視して」と言われれば,
2次までを求めるのが普通ですが,結果を見ると3次まで含めていたので,
上の計算には3次まで入れて,その結果に合うようにしたというところです.
この問題の場合,3次を無視すると結果的に1次までになってしまいますしね.
Re: ありがとうございます.
山本明 さんのレス (2005/06/05(Sun) 21:31)
「3次以上の項を無視」といってるのは, 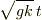 に対してですね.
に対してですね.
 の3次以上を無視するというわけではないようですよ.
の3次以上を無視するというわけではないようですよ.
Re: ありがとうございます.
tomo さんのレス (2005/06/05(Sun) 21:45)
こんばんは.tomoです.
山本さん,フォローありがとうございます.
確かに「3次以上の項を無視」は 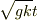 に対してです.
No.5472の私の計算では
に対してです.
No.5472の私の計算では 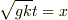 として,
これの3次まで取った結果が,テキストの解答と一致しています.
つまり,「
として,
これの3次まで取った結果が,テキストの解答と一致しています.
つまり,「 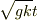 の4次以上の項を無視」しているのだと思うのですが,違うのでしょうか?
の4次以上の項を無視」しているのだと思うのですが,違うのでしょうか?
すみません,だんだん分からなくなってきました (^^;
Re: ありがとうございます.
山本明 さんのレス (2005/06/05(Sun) 23:24)
上の書き込みでいうところの 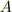 の部分も考えて,値の大きさを判断しないといけないんじゃないでしょうか.
の部分も考えて,値の大きさを判断しないといけないんじゃないでしょうか.  (=
(= 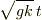 )の値は小さくても,
)の値は小さくても, 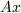 の値が小さいとは限りません.
の値が小さいとは限りません.
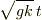 の値が3次以上を無視できるくらい小さいということは,例えば
の値が3次以上を無視できるくらい小さいということは,例えば  がすごく小さいのかもしれませんよね.とすると,
がすごく小さいのかもしれませんよね.とすると, 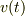 の式に現れる
の式に現れる 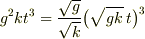 の部分は,かなり大きい値かもしれません.分母に
の部分は,かなり大きい値かもしれません.分母に 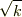 があるから.
があるから.
Re: ありがとうございます.
tomo さんのレス (2005/06/06(Mon) 00:21)
こんばんは.
山本さん,ありがとうございました.
> 上の書き込みでいうところのAの部分も考えて,値の大きさを判断しないといけないんじゃないでしょうか.
これは納得できます.でも難しいです (^^;
 の3次まで,というのは普段よく考えることですが,
の3次まで,というのは普段よく考えることですが,
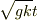 の3次まで,というのは考える機会が少ないもので,勉強になりました.
の3次まで,というのは考える機会が少ないもので,勉強になりました.
いろいろお世話になりました.
k.s さんのレス (2005/06/06(Mon) 00:32)
tomoさん,またまた親切なレスありがとうございました. 山本さんはじめまして.詳しい解説ありがとうございました. お二人のご尽力のおかげで,この問題を解決できそうです. また,疑問がでたときに質問させていただくかもしれませんがその時はまたよろしくお願いします.