ベクトルの外積を含む微分方程式
ベクトルの外積を含む微分方程式
yukihiro さんの書込 (2005/06/01(Wed) 09:01)
こんにちはyukihiroです. ボールの運動シミュレーションを行うにあたり, どうにも解けない問題にぶち当たったので,ヒントをいただければと思います.
球が回転しながら空気中を飛んでいるとき, 回転ベクトルと球の速度ベクトルとの外積の方向に力を受けます. マグヌス効果というそうです.
初期位置と初速,および回転ベクトルがわかっているとき, 任意の時刻における速度と位置を算出したいため,以下の運動方程式を立てました. 空気抵抗は速度に比例するものとし,とりあえず風速は0とします.
md<b>V</b>/dt = m<b>G</b> - k<b>V</b> + s<b>V</b>×<b>R</b> ・・・(1) m:質量 <b>V</b>:速度ベクトル t:時刻 <b>G</b>:重力加速度ベクトル k:空気抵抗係数 s:マグヌス効果係数 <b>R</b>:回転ベクトル
これを整理すると d<b>V</b>/dt = a<b>V</b> + <b>V</b>×<b>B</b> + <b>C</b> ・・・(2) a:定数 <b>B</b>,<b>C</b>:定ベクトル と表せますが, 一般にこのような微分方程式を解くにはどうしたらよいのでしょうか?
スカラーvの場合は dv/dt = av + biv + c ・・・(3) a,b,c:定数 i:虚数単位
を解くと v = (v 0 + u)e at e bit - u ・・・(4) v 0 :初速 u:= c / (a + bi) = c(a - bi) / (a 2 + b 2 ) = (ac - cbi) / (a 2 + b 2 ) e:自然対数の底
が得られるので,これを(2)式のベクトルの場合にあてはめると e bit の乗算は回転とみなせるのではと思い,以下のようにしてみました. <b>V</b> = (<b>V</b> 0 + <b>U</b>)e at M(<b>B</b>t) - <b>U</b> ・・・(5) <b>V</b> 0 :初速度ベクトル <b>U</b>:= (a<b>C</b> - <b>C</b>×<b>B</b>) / (a 2 + |<b>B</b>| 2 ) M(<b>B</b>t):<b>B</b>/|<b>B</b>|を回転軸とし,|<b>B</b>|tラジアン回転させる変換行列
実際これをプロットしてみると,<b>V</b>と<b>R</b>が垂直な場合しかそれらしい動きを見せませんでした.
四元数をうまく使えばできそうな気がするのですが, 答えを導くに至りませんでした.
長々と書いてしまいましたが,要するにお聞きしたいのは(2)の微分方程式を解く方法です. どうか救いの手を・・・
Re: ベクトルの外積を含む微分方程式
Joh さんのレス (2005/06/01(Wed) 17:19)
成分に分けちゃ,ダメでしょうか?
Re: ベクトルの外積を含む微分方程式
yukihiro さんのレス (2005/06/01(Wed) 20:36)
お二方ありがとうございます.
例えば(2)式のもっと単純な場合,a=0,<b>C</b>=零ベクトルの場合を考えると d<b>V</b>/dt = <b>V</b>×<b>B</b> となりますが,成分分解するということは, <b>V</b>のx成分をVxと表すとすると dVx/dt = VyBz - VzBy dVy/dt = VzBx - VxBz dVz/dt = VxBy - VyBx ということでしょうか?
これはどうやって解くのでしょうか?
Re: ベクトルの外積を含む微分方程式
Joh さんのレス (2005/06/01(Wed) 23:12)
積分変数がtですので,とりあえず,右辺をtが見える形に書き直してみてはどうでしょうか.
Re: ベクトルの外積を含む微分方程式
yukihiro さんのレス (2005/06/02(Thu) 08:27)
tが見える形・・・
dVx/dt = Bz∫(dVy/dt)dt - By∫(dVz/dt)dt ということ・・・か・・な・・??
ごめんなさい.頭が固いもので展望が見えてないです・・・ よかったらもう少しだけ噛み砕いてご教示いただければ・・・
Re: ベクトルの外積を含む微分方程式
Joh さんのレス (2005/06/02(Thu) 10:25)
すみません.いい加減なことを書いたかも知れません.Vの関数形は,全然分かってないのですね.
では,行列で表してみるのはどうでしょう?
Re: ベクトルの外積を含む微分方程式
崎間 さんのレス (2005/06/02(Thu) 11:13)
yukihiroさん,Johさん こんにちは.横槍すいません. せっかくシミュレーションするのですから, 直接数値計算しちゃうのはどうでしょうか.
とか
が参考になると思います.
Re: ベクトルの外積を含む微分方程式
toorisugari no Hiro さんのレス (2005/06/02(Thu) 19:23)
通りすがりのHiroです.
>これを整理すると >dV/dt = aV + V×B + C ・・・(2) >a:定数 >B,C:定ベクトル >と表せますが, >一般にこのような微分方程式を解くにはどうしたらよいのでしょうか?
両辺を 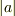 で割って改めて
で割って改めて
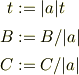
とし, 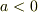 で有ることに注意すると
で有ることに注意すると
 になります.
になります. 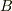 が定数ベクトルならば
が定数ベクトルならば 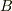 の方向に
の方向に
 軸をとれば
軸をとれば 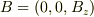 とできるので,成分で展開してください.
行列
とできるので,成分で展開してください.
行列 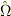 を
を
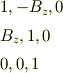
で定義するなら
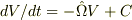 となり,
となり, 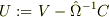 とすれば
とすれば
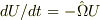 と簡単になります.
と簡単になります.  成分は自明ですし,
成分は自明ですし, 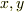 成分は
特性方程式(ケリーハミルトン)
成分は
特性方程式(ケリーハミルトン)
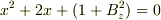 より
微分方程式
より
微分方程式
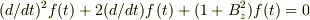 の解となります.
の解となります.
Re: ベクトルの外積を含む微分方程式
yukihiro さんのレス (2005/06/03(Fri) 07:17)
皆さんありがとうございます.
>Johさん 行列で・・・少し考えてみます.
>崎間さん ルンゲクッタ法を検討したこともありましたが, この方法だと逐次的にしか値を算出できないので 任意の時刻における速度や位置を定数時間で求めたいという ニーズには合わないと思い,使用しない方向でいました.
が,結局アニメーション表示をさせる以上, 一定の細かさで段階的に位置を算出する必要があるわけで, それならルンゲクッタ法でもいいかなと思い始めました. これなら微分方程式が複雑になっても (たとえば球の回転速度が空気との摩擦で減衰するとか・・・) あらたにそれを解く処理を追加しなくてもいいわけですし.
あらためて検討させていただきます. ていうか巷の3D物理シミュレーションではこれが一般的なんでしょうかね.
>Hiroさん なかなか難解ですね^^;
微積分の知識があまりないので, 突然特性方程式が出てくるところがよくわかりませんでした.
そこはおいておくとして, x 2 + 2x + (1 + B z 2 ) = 0 は虚数解 x = -1±B z i を持つので, 示された微分方程式の解は(大学時代の微積の教科書によると)
f(t) = e -t (C 1 cos(B z t) + C 2 sin(B z t)) C 1 ,C 2 :積分定数
となるわけですが, 2つの積分定数はどうやって決定するんでしょう? t=0において<b>V</b>=<b>V</b> 0 という1つの初期条件しかないわけですが・・・
Re: ベクトルの外積を含む微分方程式
yukihiro さんのレス (2005/06/03(Fri) 08:29)
追伸 座標軸を取り直すというアイデアはいいヒントになった気がします. このアイデア自体はこの「物理のかぎしっぽ」にもありましたね.
「角速度と速度との関係」
これを応用することを思いつかなかった自分の頭の固さを実感します. ていうか少し難解でちゃんと読んでなかったのが悪いのかもしれませんが.
Re: ベクトルの外積を含む微分方程式
yukihiro さんのレス (2005/06/03(Fri) 08:47)
何度もすいません.
> 2つの積分定数はどうやって決定するんでしょう? > t=0においてV=V0という1つの初期条件しかないわけですが・・・
何となくですが, C 1 = C 2 としてかまわない気がしてきました. 根拠はちゃんと説明できないですが, 何となくそんな匂いがしたもので.
Re: ベクトルの外積を含む微分方程式
おこめ さんのレス (2005/06/03(Fri) 11:34)
どうもはじめましてyukihiroさん.理学部の学部3年のものです.記事の引用ありがとうございます(この記事を持ち込んだ者です).
>・・・ていうか少し難解
すみません.改訂をしようとは思っているのですが・・・
>2つの積分定数はどうやって決定するんでしょう?
ですが,これは2つの条件を与えれば良いと思います(これがシュミレーションする内容を示すパラメータの一部では?1自由度あたり2つの積分定数,あと定ベクトル2つと1つのスカラーですから自由度3の運動をシミュレーションすれば計13個のパラメータでしょうか?).他のパラメータを固定したとすると,1自由度あたり2つの独立な運動条件のみが,運動のバリエーションを与えていていると思います.仮にこれが任意の状況で完全に決まってしまったら,どんな状況でも同じ運動をしてしまうという何ともおかしな状況になってしまいそうです.
たとえば,初期速度と初期位置のみで運動(軌道)が完全に決まると思えば良いのではないですか(初期位置,初期速度が違うのに同じ軌道を描くのが正しくないのはシミュレーションせずとも分かると思います)?
Re: ベクトルの外積を含む微分方程式
toorisugari no Hiro さんのレス (2005/06/03(Fri) 19:15)
> 突然特性方程式が出てくるところがよくわかりませんでした えっと,たとえば
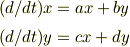
という微分方程式を考えます.  を消去して
を消去して  だけの式に
したいのですが,結構大変です.
でも行列
だけの式に
したいのですが,結構大変です.
でも行列 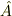 を
を
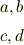
とすれば上の式は
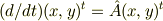
とかけます.(  は転置)
ここで,
特性方程式は
は転置)
ここで,
特性方程式は 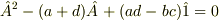 ですから,
ですから,
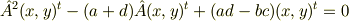
であり,結果
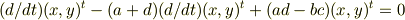
がえられます.
あと,初期条件ですが,  で2個,
で2個,  で2個の計4個
でますが,方程式に代入すれば2個減るので最終的には2個となり,
で2個の計4個
でますが,方程式に代入すれば2個減るので最終的には2個となり, 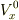 ,
, 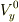 を与えれば完全に決まります.
を与えれば完全に決まります.
Re: ベクトルの外積を含む微分方程式
おこめ さんのレス (2005/06/03(Fri) 22:12)
上の解説は特性方程式自体の意味が分からなければ厳しそうです(よく読んでませんが,はじめから連立方程式を考えているみたいなので).簡単のために定数係数線形微分方程式
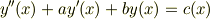
の解を求めるときを考えます.簡単のためにまず 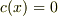 の場合を考えて,解を初等関数の一般形
の場合を考えて,解を初等関数の一般形 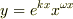 と仮定します(線形性から考えて妥当な仮定だと思います).これを上の方程式(ただし
と仮定します(線形性から考えて妥当な仮定だと思います).これを上の方程式(ただし 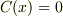 )に代入すれば,特性方程式が得られると思います.数学的に正確な説明かは分かりませんが,とりあえず正しい結果は得られます.あとはこの同次形の解から定数変化法で求めるなりすれば上の方程式の一般解が求まると思います.
)に代入すれば,特性方程式が得られると思います.数学的に正確な説明かは分かりませんが,とりあえず正しい結果は得られます.あとはこの同次形の解から定数変化法で求めるなりすれば上の方程式の一般解が求まると思います.
的外れなら書き込みならば,どうぞ無視してください.お願いします.
Re: ベクトルの外積を含む微分方程式
Joh さんのレス (2005/06/04(Sat) 00:43)
線形なので,微分は,演算子の掛け算だと思って良いのです.そう思えば,ただの二次方程式と,似たようなものなわけです.行列で,ケーリー=ハミルトンの公式というのがあったのは大丈夫でしょうか.
Re: ベクトルの外積を含む微分方程式
yukihiro さんのレス (2005/06/04(Sat) 18:15)
皆さんありがとうございます.
特性方程式自体は多分高校レベルの話でしたね. すっかり失念してました. それと連立微分方程式の関係もおかげさまで理解できました.
初期条件についても,Hiroさんのおっしゃるとおり連立方程式に代入することにより, 4つの積分定数を確定することができました.
おかげさまで,期待通りの動作をさせることが・・・ できました,と言いたいところですが, 初期条件によって微妙に変な動きをするので現在デバッグ中です.
上記積分定数を求める過程でどっか計算違いをしたかな?などと思ってますが, とりあえず都合により今日明日は進展しそうにないので, また明後日あたりに報告したいと思います.
Re: ベクトルの外積を含む微分方程式
yukihiro さんのレス (2005/06/07(Tue) 15:18)
遅くなりましたが,結果報告させていただきます.
計算が多少複雑なので ・机上の計算にミスがないか ・それを正しくコードに落とせているか というチェックに手間取り,デバッグにかなり苦労しましたが ようやく期待通りの動作をさせるに至りました. 苦労した分喜びも一入といったところでしょうか^^;
ちなみにバグの内容は,やはり積分定数の計算違いもありましたが, それに加えてBの方向をZ軸にとるという座標変換についてもミスってましたorz
ここで結論だけまとめておきたいと思います.
> d<b>V</b>/dt = a<b>V</b> + <b>V</b>×<b>B</b> + <b>C</b> ・・・(2) > a:定数 > <b>B</b>,<b>C</b>:定ベクトル
の解は以下のようになります.
以降すべて<b>B</b>の向きがZ軸正方向になるよう座標を取り直したものの結果で,<b>B</b>≠零ベクトルとします. またx,y,zはベクトルのx,y,z成分を表します.
Vz(t) = (V 0 z + Cz / a)e at - Cz / a (a ≠ 0) Vz(t) = tCz + V 0 z (a = 0)
Vx(t) = (D 1 cosbt + D 2 sinbt)e at - Ex Vy(t) = (D 2 cosbt - D 1 sinbt)e at - Ey b = |<b>B</b>| D 1 = V 0 x + Ex D 2 = V 0 y + Ey <b>E</b> = <b>C</b>Ω -1 Ω = a-b0 b a0 0 0a ※ここで示すΩはHiroさんの示されたΩをa倍して転置したものになります.
V(t)を積分した位置ベクトルP(t)については以下のようになります.
Pz(t) = (V 0 z + Cz / a)e at / a - tCz / a - (V 0 z + Cz / a) / a + P 0 z (a ≠ 0) Pz(t) = t 2 Cz / 2 + tV 0 z + P 0 z (a = 0)
Px(t) = {(aD 1 - bD 2 )cosbt + (bD 1 + aD 2 )sinbt}e at / (a 2 + b 2 ) - tEx - (aD 1 - bD 2 ) / (a 2 + b 2 ) + P 0 x
Py(t) = {(aD 2 + bD 1 )cosbt + (bD 2 - aD 1 )sinbt}e at / (a 2 + b 2 ) - tEy - (aD 2 + bD 1 ) / (a 2 + b 2 ) + P 0 y
最後に座標軸を元に戻して完了です.
ある程度予想してましたが,回転速度(orマグヌス効果係数)を上げると非常に面白い軌跡を描きますね.
崎間さん,Johさん,Hiroさん,おこめさん,本当にありがとうございました.
Re: ベクトルの外積を含む微分方程式
おこめ さんのレス (2005/06/07(Tue) 19:20)
計算は追っていませんが,うまくいったようで良かったです.
No.5448を読んで,僕は定数を完全に決めようとしているのかと誤解してしまいました.それで僕は,勘違いな事を2回ほど書いていただけです.どうもご迷惑をおかけしました.
Re: ベクトルの外積を含む微分方程式
やかん さんのレス (2005/06/08(Wed) 15:07)
yukihoroさん,はじめまして.解決したようでよかったですね. ベクトル,行列の演算は私にはお手上げなのですが 最近読んだ岩波科学ライブラリーの”魔球を作る”という書籍に 野球の変化球の原因は,ボールの回転による,流体である空気との間に生じる マグナス力だと書いてあったので,きっとその力のことかなあ,なんて 想像しました.その本には”直球は変化球?!”と書いてあって 直球はバックスピンの回転がかかっているため上向きにマグナス力が働き 空気中での放物線(て言わないか・・)よりも浮いている(落ちていない)そうですね. 一方フォークボールは回転がほとんどなく,自然の落下にちかいから, フォークボールは変化球ではないそうです.混ぜて投げると,フォークボールの方が ”落ちる球”とバッターには見えるとか・・・.ところでyukihiroさんがお書きの 指数や添字はどうやっていらっしゃるのでしょうか.texではないような・・・.
Re: ベクトルの外積を含む微分方程式
yukihiro さんのレス (2005/06/08(Wed) 17:17)
>おこめさん 迷惑なんてとんでもないです. とても勉強になりました. No.5448は気にしないでください. 私のいい加減な嗅覚が露呈した恥ずかしいレスなので;;
>やかんさん
> 最近読んだ岩波科学ライブラリーの”魔球を作る”という書籍に
これですね.
著者のインタビュー記事です.
私もいろいろ調べているときにこのページにも辿り着き, 興味深く読ませてもらいました. あんなちょっと出っ張ってるだけのシームがそんなに軌道に影響を与えるものなんですね. 巨人の星の消える魔球も可能などと豪語されてますが,信じていいんですかねw 書籍のほうもちゃんと読んでみたいところです.
> ところでyukihiroさんがお書きの > 指数や添字はどうやっていらっしゃるのでしょうか.texではないような・・・.
「利用上の注意」に書いてありますよ^^;
私の計算式,読み辛くて申し訳ないです. 本当はTeX数式を使いたかったのですが,未経験者には少し敷居が高くて・・・ この掲示板,プレビュー機能をつけていただくわけにはいかないかな,とかわがままを言ってみたり.
Re: ベクトルの外積を含む微分方程式
やかん さんのレス (2005/06/08(Wed) 19:56)
>これですね.
著者のインタビュー記事です.
うわー,この先生,結構本の中身しゃべっちゃってますね. きっと学術一筋で,儲けがどうこうなんて考えないのかな :)
>私もいろいろ調べているときにこのページにも辿り着き, 興味深く読ませてもらいました.
すみません・・,ご存知とは知らずに,私ちょっと知ったかぶりしちゃったみたいです.
>巨人の星の消える魔球も可能などと豪語されてますが,信じていいんですかねw
そっかー,これがあるから購買欲がまだまだそそられますね (^^;
>書籍のほうもちゃんと読んでみたいところです. 私は理解できなかったのですが,結構数式とか多いので,お読みになられると きっと面白いのではないかと思います.
>「利用上の注意」に書いてありますよ^^;
=howto 本当はTeX数式を使いたかったのですが,未経験者には少し敷居が高くて・・・
あっ,そうだ!tex以前に使えるようにしていただいたんだった・・.私としたことが. でも簡単な表記だったらなんと私でもできるのだから,yukihiroさんだったら絶対使えちゃいますよ. :)