質問
質問
zak さんの書込 (2005/05/25(Wed) 20:08)
出典:単位が取れる電磁気学ノート
半径aの導体球Aと,それをとりまく内径bの同心導体球殻Bでコンデンサーをつくる.導体球殻Bは薄くて,外径もbとみなせるものとする.次の場合について,このコンデンサーの電気容量を求めよ.ただし,導体球Aと導体球殻Bの間の空間は真空で真空の誘電率をε0とする.
問:導体球殻Bに電荷を与え,導体球Aを接地する.
解説:導体球殻Bに電荷をQを与える.そして,外面と内面の両方に電荷が分布する.なので,導体球Aに導かれる電荷の量は,Qより小さい.球殻の内面に分布する電荷をQ'とする.すると,導体球Aに導かれる電荷はーQ'となる.
AとBの間の空間(a≦r≦b)の電位を計算すると,
V(r)=Q'(1/a-1/r)÷4πε0
で,導体球殻Bの外側(b≦r)の空間の電位は,
V(r)=Q-Q'/4πε0
となる.
・・・・・・・・・・・・・・・・ この後,電位差を求めて,容量を求める.
疑問点:導体球殻Bの外側(b≦r)の空間の電位は
E=-dV/drより,V=-∫Edrとなります.これは,不定積分なので計算すると
V(r)=Q-Q'/4πε0 + α←これがつきませんか?
参考書では,ただ単にV(r)=Q-Q'/4πε0しか書いてません.定数が無いと,球殻のBの内部と外部の電位が球殻Bにおいて等しいという条件でr=bで等しいとして代入しなければいけません.どうして,積分定数のαがつかないのでしょうか?もしくは,参考書が間違っているのでしょうか.その他の求め方はわかります.お願いします.
Re: 質問
崎間 さんのレス (2005/05/26(Thu) 01:03)
> V(r)=Q-Q'/4πε0しか書いてません.
分母に r が抜けているようです.V(r)=(Q-Q')/(4πε_0 r) ですよね?
> 定数が無いと,球殻のBの内部と外部の電位が球殻Bにおいて等しい > という条件でr=bで等しいとして代入しなければいけません.
これまでに同様の処理が続いているので,その処理を端折って結果だけを載せているのではないでしょうか.確かに
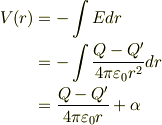
と,積分定数  がつくのが正しいですが,
がつくのが正しいですが, 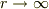 で
で 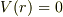 を考えると
を考えると 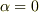 になります.でも,少し分かりにくい部分であるかもしれません.参考書を「間違いではないか」と考えながら読む zak さんの姿勢は賛成です :)
になります.でも,少し分かりにくい部分であるかもしれません.参考書を「間違いではないか」と考えながら読む zak さんの姿勢は賛成です :)
Re: 質問
zak さんのレス (2005/05/26(Thu) 22:41)
返信ありがとうございます.すいません,rが抜けてました,,,.
たしかに,積分定数つきますよね.自分もr=∞の時にV(r)=0になると思ったんですが,r=aでこの場合Vが0になってますよね?r=aの時V=0になるのに,r=∞のときも0になるんでしょうか,,,.
Re: 質問
崎間 さんのレス (2005/05/27(Fri) 10:15)
> r=aの時V=0になるのに,r=∞のときも0になるんでしょうか,,,.
確かその参考書に,電位と距離のグラフがありますよね.そのグラフからみても,r=a と r→∞ で V=0 になるのは自然なことだと思います.
Re: 質問
山本明 さんのレス (2005/05/27(Fri) 11:38)
電位というのは,どこかしらに基準を設けないと測れません.
だから不定積分じゃなくて,どんな場合も定積分になります.基準点を 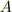 と書いたら,
と書いたら,
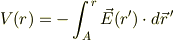
ということ.
崎間さんが書いてる  というのは,基準点での電位ということになります.その基準点として,電位が0になるような場所を選べれば,電位の表記が単純になります.そうなると嬉しいので,大抵の場合には無限遠点を基準に設定するというわけです.
特に指定もなく「電位」と書かれていたら,「無限遠点を基準にした電位」と考えるのが無難でしょう.
ちなみに無限遠点を電位の基準とするのは,無限遠点では電位が0だろう!という前提があるわけですが,問題設定によっては必ずしも無限遠点が電位0にはなりません.無限に長い棒状に電荷が分布しているとか,無限に広い平面上に電荷が分布している場合なんかは,無限遠点の電位が0にならないので,無限遠点を基準にした電位を求めることはできません.
というのは,基準点での電位ということになります.その基準点として,電位が0になるような場所を選べれば,電位の表記が単純になります.そうなると嬉しいので,大抵の場合には無限遠点を基準に設定するというわけです.
特に指定もなく「電位」と書かれていたら,「無限遠点を基準にした電位」と考えるのが無難でしょう.
ちなみに無限遠点を電位の基準とするのは,無限遠点では電位が0だろう!という前提があるわけですが,問題設定によっては必ずしも無限遠点が電位0にはなりません.無限に長い棒状に電荷が分布しているとか,無限に広い平面上に電荷が分布している場合なんかは,無限遠点の電位が0にならないので,無限遠点を基準にした電位を求めることはできません.
いま問題設定で,r=aのところを接地しているようです. その場合,r=aの位置と無限遠点とが同じ電位になるように電荷分布が起きます.それが「接地した」ということ.だからr=aのVもr→∞のVも0になるでしょう. 実際に接地したことで起きる電荷分布に従って計算して電位を求めたら,ちゃんと接地した位置と無限遠点とが同じ電位になっているでしょう.(なっていなかったら,電荷分布の予測を間違えたか計算ミスしたかのどちらかでしょう)
Re: 質問
崎間 さんのレス (2005/05/27(Fri) 17:10)
山本さん,フォローどうもありがとうございます m(_ _)m
Re: 質問
zak さんのレス (2005/05/28(Sat) 19:41)
山本さん,崎間さんお答えいただきありがとうございます.理解できました.よく考えてみるとやはり,V=0ですよね,,,.勉強不足です.ありがとうございました!