ちょっとバカみたいな質問なんですが・・・
ちょっとバカみたいな質問なんですが・・・
kou さんの書込 (2005/05/24(Tue) 21:03)
初めまして!kouと申します.高校生です. 先日物理学について少し興味を持ったので質問させていただきます. 興味を持ったのはいいのですが,物理学を全くやったことがありません; これからも掲示板を使わせていただきたいので,少しずつ教えてもらえたらうれしいです. それで,質問です・・・物理学にはいろいろ種類があるみたいですが,初心者はどこから勉強すればいいのか全くわかりません.どんな種類があるのかもまだわかりません.検索サイトで調べてみたのですが,物理学の種類をまとめたサイトもありません.どうか教えていただけたらうれしいです. お願いします.
Re: ちょっとバカみたいな質問なんですが・・・
Joh さんのレス (2005/05/24(Tue) 22:32)
kouさんこんにちは
種類というのは分け方次第でいくらでもあるので, 網羅するというのは無理です. また,相互にどの分野も関連していますので,境界上 にあるような勉強は,分類できないということもあります. 物理を専門にしている人でも,自分の分野以外のことは あまり分からない,という人が多いのです.
しかし,基礎になる部分は,おおまかに ・力学 ・熱力学 ・電磁気学 ・量子力学
のような分野に分かれています.力学が基礎ですので, 力学からやるのが普通です.
では,頑張って下さい.
早速ありがとうございます
kou さんのレス (2005/05/24(Tue) 22:39)
Jhoさんありがとうございます.
実は興味を持ったきっかけは力学なんです. 答えを出すまで頑張ったのですが,途中でわからくなってしまいました.問題がすごくバカらしいんですけどね(笑)
やっぱり物理学は数学も重要になりますよね?
あと,勉強するためにはやはり参考書などが必要になりますよね?
Re: 早速ありがとうございます
やかん さんのレス (2005/05/25(Wed) 00:57)
kouさん,はじめまして.Johさん,こんにちは.
>答えを出すまで頑張ったのですが,途中でわからくなってしまいました.問題がすごくバカらしいんですけどね(笑)
そのバカらしい問題,学校の宿題とかでなければ,頑張ったところまで教えていただけませんか?もしわからない問題がわかるようになったら嬉しいですよ,きっと. :)
Re: ちょっとバカみたいな質問なんですが・・・
kou さんのレス (2005/05/25(Wed) 08:35)
校舎の3階(高さ15m)から中庭を通して(距離20m)1階の飛び出した屋根(高さ5m)まで飛ぶのには,最低時速何kmで飛び出せば1階の屋根まで飛べるか
です.力学未経験なので,頭の中にイメージできるだけで最後まで解けません. 分かりやすく教えてもらえれば嬉しいです.
Re: ちょっとバカみたいな質問なんですが・・・
崎間 さんのレス (2005/05/25(Wed) 09:38)
高さ 15m から高さ 5m 落下するまでの間に,水平に 20m 移動できれば隣の屋根まで飛び移ることができます.高さ 15m から高さ 5m まで落ちるのですから,10m 落ちます.10m だけ落下するまでにかかる時間を  とします.この
とします.この  は,投下速度運動の式から求めることができます.
は,投下速度運動の式から求めることができます.  の間に 20m 移動するのに必要な速度が,求める値です.
の間に 20m 移動するのに必要な速度が,求める値です.
> 初心者はどこから勉強すればいいのか全くわかりません.
「初心者は,物理のかぎしっぽで勉強すれば大丈夫です!」と胸を張って言えるようになりたいものです.最近記事を書いていないので,なんとかしなきゃと思ってはいるのですがー.
Re: ちょっとバカみたいな質問なんですが・・・
やかん さんのレス (2005/05/25(Wed) 10:14)
崎間さん,有難うございます.kouさん,ヒントがもらえて良かったですね. いきなり解答よりも,少しづつ一緒に考えながらの方が,実力つくし,楽しいです. また,わかったり,考えてもわからなかったりしたら,書き込んでくださいね. 崎間さんが,おっしゃった式,ご存知ですか?物理の教科書は持ってますか?
崎間さん,やかんさん,返信ありがとうございます
kou さんのレス (2005/05/25(Wed) 13:33)
崎間さん,やかんさん返信ありがとうございます.
崎間さん,頭の中でイメージは作れるんですけど…家に帰ったら図に書いてみます.
やかんさん,皆さんと一緒に少しずつ解いて,理解していけたら嬉しいです. それで,うちの高校は商業高校なので物理を勉強するかもわかりません. なので,物理の教科書もありませんし,式も全然わかりません.ホントに1からスタートですので,教えてもらえたら嬉しいです.
Re: 崎間さん,やかんさん,返信ありがとうございます
やかん さんのレス (2005/05/25(Wed) 16:55)
>皆さんと一緒に少しずつ解いて,理解していけたら嬉しいです. 一緒に楽しく頑張りましょう.私も物理は高校でちょっとやったきりで 大学では勉強していないのでよくわかりませんが,それでも大好きです. インターネットで自由落下,と引いてみたら,以下のようなページがありましたが ちょっと見てみません?
もしかして文字ばっかりでウンザリでしょうか?難しく感じますか?大丈夫,大丈夫.
地球にある物はなんでも地球から引っ張られます.例えばリンゴも木から落ちるし,ボールを水平に投げたつもりでもいつか地面に落ちます.地球が物を引っ張る割合は決まっていて,1秒間に物が増す速度(加速度)が一定です.距離じゃなくて速度自体が増すんですよ.段々スピードアップするという事です.例えば最初に速度0m/秒のものが1秒間に10m/秒づつスピードアップしていくと,1秒後に速度10m/秒,2秒後に20m/秒,3秒後に30m/秒,・・・とじゃんじゃん速くなりますよね.このスピードの増し方だと,3秒でどれだけの距離進むでしょうか?
3秒後が速度10x3(=30)m/秒なので,3x30で90mでしょうか?いいえ,違います.速度は最初0で,30m/秒になったのは最後の一瞬だけ,だから平均すれば(0+30)÷2=15で,平均速度はわずか15m/秒です.つまり,距離は15x3=45,45mということになります.ここまで
わかりますか?上の例では1秒間に増す速度(加速度)を10m/秒としましたが,地球の重力加速度は1秒間に約9.8m/秒です(これを 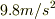 と書きます).ここで中学の方程式のように数字の変わりに文字を入れてみましょう.加速度(上の例で10と言っていた)を
と書きます).ここで中学の方程式のように数字の変わりに文字を入れてみましょう.加速度(上の例で10と言っていた)を  ,何秒間かかるか(上では3と言っていた)を
,何秒間かかるか(上では3と言っていた)を  ,とすると,進む距離(落ちた高さ)は
,とすると,進む距離(落ちた高さ)は
 と
と  ,でどうあらわせるでしょうか?ちょっと考えてみてください.
,でどうあらわせるでしょうか?ちょっと考えてみてください.
Re: 崎間さん,やかんさん,返信ありがとうございます
kou さんのレス (2005/05/25(Wed) 18:18)
やかんさんこんにちは.
やっぱり物理初体験なので,少し難しいです.もともとあまり数学が得意ではなので・・・;
>例えば最初に速度0m/秒のものが1秒間に10m/秒づつスピードアップしていくと,1秒後に速度10m/秒,2秒後に20m/秒,3秒後に30m/秒,・・・とじゃんじゃん速くなりますよね.このスピードの増し方だと,3秒でどれだけの距離進むでしょうか? 3秒後が速度10x3(=30)m/秒なので,3x30で90mでしょうか?いいえ,違います.速度は最初0で,30m/秒になったのは最後の一瞬だけ,だから平均すれば(0+30)÷2=15で,平均速度はわずか15m/秒です.つまり,距離は15x3=45,45mということになります.ここまで わかりますか? ということは,例えば10秒間になると・・・10秒間には100m/秒ですよね?最初は0で最後の一瞬は100m/秒→平均すると・・・(0+100)÷2=50mですか?ということは,平均速度が50m/秒となるのですよね?
>地球の重力加速度は1秒間に約9.8m/秒です(これを 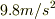 と書きます).
と書きます).
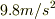 が地球の重力加速度・・・sというのは英語の秒のことですよね?2とは二乗のことですか?なぜ二乗をするかさえわかりません・・・;
が地球の重力加速度・・・sというのは英語の秒のことですよね?2とは二乗のことですか?なぜ二乗をするかさえわかりません・・・;
上の例を地球上でやってみると,10秒間で98m/秒ということですよね.そしてこれを平均すると・・・平均速度は49m/秒ですか?こんな感じでいいのですかね?
>進む距離(落ちた高さ)はと,でどうあらわせるでしょうか?ちょっと考えてみてください.
小学校くらいに教わったみ・は・じを使えば(使っていいのですか?),速さ→  ,時間→
,時間→  道のり(距離)→
道のり(距離)→ 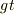 (g×t)であらわせるということですか?
(g×t)であらわせるということですか?
疑問ばかりですいません
Re: 崎間さん,やかんさん,返信ありがとうございます
Joh さんのレス (2005/05/25(Wed) 18:47)
kouさん,
物理をやるには,多少の数学は必要ですが, 一番大事なのは,現象をイメージすることと, 何か面白い現象があったときに,面白い!と 感じるハートです.それだけあれば大丈夫.
例えば,自動車の速度の単位がkm/hとかだというのはご存知ですよね. 『一時間当たり,何キロ進むか』ということで, キロが,時間で割ってあるわけです.kouさんが 小学校で習った式ですね.
いま,キロと時間じゃなくて,メートルと秒で, 速度の単位はm/sということにしておきます.
加速度は,『一秒間(s)に,どれくらい速度vが増すか』 ということなので,さっきと同じようにv/sと書けます. ここで,速度の単位がm/sだったので,vのところに m/sを代入して見てください.m/s2になります.
分からなかったら,また質問してください. 力学は,私の一番好きな分野です.
Re: 崎間さん,やかんさん,返信ありがとうございます
やかん さんのレス (2005/05/25(Wed) 18:58)
おお,なかなかいいじゃないですか.
>ということは,例えば10秒間になると・・・10秒間には100m/秒ですよね?最初は0で最後の一瞬は100m/秒→平均すると・・・(0+100)÷2=50mですか?ということは,平均速度が50m/秒となるのですよね?
そういう事です!とにかく今はわかりやすくそう考えておきましょう.
> 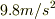 が地球の重力加速度・・・sというのは英語の秒のことですよね?2とは二乗のことですか?なぜ二乗をするかさえわかりません・・・;
が地球の重力加速度・・・sというのは英語の秒のことですよね?2とは二乗のことですか?なぜ二乗をするかさえわかりません・・・;
その通り,sは英語のsecondの略で,秒を表す単位です.ところで,ちょっと寄り道.
縦2m,横3mの花壇の面積は,6 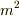 と書きますよね?この
と書きますよね?この 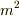 は
もちろん面積の単位ですが,どう見てもmの2乗と書いてある・・.なんで??
これは計算する時にmを2回かけているからです.2(メートル)x3(メートル)=
6(メートルの2乗)=6
は
もちろん面積の単位ですが,どう見てもmの2乗と書いてある・・.なんで??
これは計算する時にmを2回かけているからです.2(メートル)x3(メートル)=
6(メートルの2乗)=6 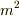 というわけです.
例えば2y x 3y =6
というわけです.
例えば2y x 3y =6 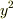 だから,mを単位ではなく,x(エックス)や,y(ワイ)のような文字と考えると,自然な気がしますよね.単位ごと,計算しちゃう感じです.ところで加速度の話ですが,1秒間に何m/s速度が増すかですから,計算はどうやりますか?例えば3秒間で,30m/s増せば,1秒間には,30÷3ですが,単位つきで計算すると
30m/s÷3sとなりますよね.ところでm/sは単位ですが,これも分数なのはわかりますか?
なぜなら速度を出す時にmをsで割るからです.m/s=
だから,mを単位ではなく,x(エックス)や,y(ワイ)のような文字と考えると,自然な気がしますよね.単位ごと,計算しちゃう感じです.ところで加速度の話ですが,1秒間に何m/s速度が増すかですから,計算はどうやりますか?例えば3秒間で,30m/s増せば,1秒間には,30÷3ですが,単位つきで計算すると
30m/s÷3sとなりますよね.ところでm/sは単位ですが,これも分数なのはわかりますか?
なぜなら速度を出す時にmをsで割るからです.m/s= 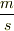 .分数の横棒を斜めに書いているだけです.そうすると加速度は
.分数の横棒を斜めに書いているだけです.そうすると加速度は 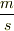 をさらにsで割るのだから,分母にsが2個掛け合わされて,
をさらにsで割るのだから,分母にsが2個掛け合わされて, 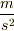 と.分数とか,2乗とか,単位を文字式みたいに一緒に計算してしまうんですね.
と.分数とか,2乗とか,単位を文字式みたいに一緒に計算してしまうんですね.
>上の例を地球上でやってみると,10秒間で98m/秒ということですよね.そしてこれを平均すると・・・平均速度は49m/秒ですか?こんな感じでいいのですかね?
そういう事です.正確には速度と加速度の関係は微分積分で表すのですが,まだその話は やめておきましょう.
>小学校くらいに教わったみ・は・じを使えば(使っていいのですか?),速さ→  ,時間→
,時間→  道のり(距離)→(g×t)であらわせるということですか?
道のり(距離)→(g×t)であらわせるということですか?
おっ,惜しい・・・.時間はOKですが,  は速度ではなくて”加速度”です.例の通りに順にやっていきましょう.加速度x時間が最後の瞬間の速度ですよね?これは,
は速度ではなくて”加速度”です.例の通りに順にやっていきましょう.加速度x時間が最後の瞬間の速度ですよね?これは,  と,
と,  でどうあらわせるでしょう?
でどうあらわせるでしょう?
Re: 崎間さん,やかんさん,返信ありがとうございます
やかん さんのレス (2005/05/25(Wed) 19:49)
Johさん,内容がだぶってしまい大変失礼いたしました. (更新前に返信送ってしまい遅くなってしまいました・・・)
Re: 崎間さん,やかんさん,返信ありがとうございます
kou さんのレス (2005/05/25(Wed) 20:29)
やかんさん,Jhoさんこんばんは.
今すごい考えてるんですけど・・・;やっぱり難しいです.多分答えがわかれば納得すると思うのですが,そこまで行くのに時間がかかるかもしれないです・・・ やかんさん,Jhoさんの書いてくださった文の中にヒントが隠れてますか?
Re: 崎間さん,やかんさん,返信ありがとうございます
Jho さんのレス (2005/05/25(Wed) 20:36)
速度というのは,ある時間の間に,どれくらい距離が 変わるか,ということですね.
加速度というのは,ある時間の間に,どれくらい速度が 変わるか,ということです.
この二つの文章を組み合わせてみると, 『加速度というのは,ある時間の間に,どれくらい 距離が変わるかが変わるか』だと言えませんか.
これが二乗になってる秘密です.余計混乱したかな.
Re: 崎間さん,やかんさん,返信ありがとうございます
kou さんのレス (2005/05/25(Wed) 21:01)
Jhoさん
>加速度は,『一秒間(s)に,どれくらい速度vが増すか』ということなので,さっきと同じようにv/sと書けます.ここで,速度の単位がm/sだったので,vのところにm/sを代入して見てください.m/s2になります.
ここを考えたら少し理解だけできたと思います. 例えば,一秒間当たりに30m進むとしたら30m/sで,これをv(速度)/s(一秒間)に代入すると速度は30m/sなのでvに代入して(30m/s)/sになるってことですよね? でも・・・この式からどうして2乗になるのですか?本当に数学ができないのでわかりません.どこにもsとsを掛ける所なんてないように見えますが・・・
Re: 崎間さん,やかんさん,返信ありがとうございます
崎間 さんのレス (2005/05/26(Thu) 01:22)
> 速度は30m/sなのでvに代入して(30m/s)/sになるってことですよね? > でも・・・この式からどうして2乗になるのですか?
「割り算」の割り算を思い出しましょう. 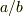 を
を  で割るには
で割るには
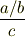
分母分子に  を掛けて
を掛けて
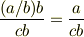
です.同じように 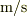 を
を  で割ってみてください.
で割ってみてください.
Re: 崎間さん,やかんさん,返信ありがとうございます
やかん さんのレス (2005/05/26(Thu) 15:00)
>今すごい考えてるんですけど・・・;やっぱり難しいです.多分答えがわかれば納得すると思うのですが,そこまで行くのに時間がかかるかもしれないです・・・
いや,学校でもやってらっしゃらなくて,特別数学が得意というのでなければ難しく感じるのは当然で,めげることないですよ!それにいきなり答えを聞いても面白くもためにもなりません.大変かもしれませんが,自分でわかったときは感激しますよー,きっと.
時間は他の勉強のじゃまにならなければ,ある程度かかってもいいのでは・・(でもいろいろお忙しいかな?).斜線も横棒も分数をあらわしていて,”右”ぶんの”左”あるいは,”下”ぶんの”上”,割り算と考えると,逆に左わる右,または,上わる下ですよね?(そのぐらい知ってらー,と思われたらすみません・・・)
崎間さんのご説明通り,例えば18/3 ÷3=18÷3÷3=18÷ 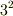 =
= 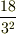 =18/
=18/ 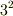 ですよね?
kouさんがせっかく出された
ですよね?
kouさんがせっかく出された 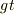 は距離ではなくて終わりの速度ですよね.
最初は速度ゼロだから,平均速度はどうですか?
は距離ではなくて終わりの速度ですよね.
最初は速度ゼロだから,平均速度はどうですか?
どうですかね・・・?
kou さんのレス (2005/05/26(Thu) 21:30)
TeX数式が難しくて使えないので見づらいですが・・・
崎間さん 今日学校でなぜ2乗になるのかを教わりました.崎間さんとはやり方が違うと思いますが,要はこういうことですかね? s/m ÷ s = s/m × s/1 = s^2/mということで,2乗になるということですよね?
やかんさん >(そのぐらい知ってらー,と思われたらすみません・・・) 分数が一番苦手なんで・・・(高校生にもなって何を言ってるんでしょうかね)
>kouさんがせっかく出された 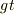 は距離ではなくて終わりの速度ですよね.最初は速度ゼロだから,平均速度はどうですか?
は距離ではなくて終わりの速度ですよね.最初は速度ゼロだから,平均速度はどうですか?
平均速度は・・・ 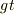 が最後の瞬間でこれを前にやった平均を出す式に当てはめれば,(0+gt)÷2 = 2/gt
これが平均を出す式ですか?
そして,距離を出す式は,2/gt × tですかね?
正解ですか?
が最後の瞬間でこれを前にやった平均を出す式に当てはめれば,(0+gt)÷2 = 2/gt
これが平均を出す式ですか?
そして,距離を出す式は,2/gt × tですかね?
正解ですか?
見づらくてすいません.
Re: どうですかね・・・?
Goodluck さんのレス (2005/05/27(Fri) 03:53)
お邪魔いたします.kouさん初めましてGoodluckと申します.よろしくお願いします.テスト期間中なので全然チェックする暇もなく掲示板の過去ログも飛ばしております.終わったら確認したいなぁ..
閑話休題
これなんですがグラフを書くというのも解法の一つとしてとても役立つと思うのですがいかがでしょうか?Y軸を速度,X軸を時間で表しまして.これでグラフを書いてみますと加速度というのはそのグラフの傾きになるのですが. こういうと余計に混乱してしまうかもしれませんね….
ビジュアルエイドというのはとても大事でして….なんかよく分からないけどグラフにすると見えてくることもあります.一度試してみてはいかがでしょうか?
それと匹敵するぐらい物理ではユニット(単位)がとても大切です.それを合わせることで自分が何をしてるのか分かったりもします.
初めて物理を勉強すると頭を理系に切り替えることがちょっと大変かもしれませんが頑張って努力してたらいつか急に分かった!というときが来ると思いますので,継続して努力してくださいね^^
>Jhoさん 誰も突っ込まないので私が….いつのまにかIDの欄までJhoさんに代わってたのには笑わせてもらいました(笑うところではない?)
>崎間さん 下のスレでTexの表示を教えていただきましてありがとうございます. 次から使わせていただきます,それとお礼が遅くなりましたことお詫びします. 失礼します.
Re: どうですかね・・・?
Jho さんのレス (2005/05/27(Fri) 08:44)
>Goodluckさん
期末試験はどうですか?僕も試験監督が 来週まであります.6月5日にマンチェスターに 行きますが,日帰りなので,今回飲みに行く時間は なさそうです.日本で飲みに行きましょう.
>kouさん
分数がんばりましょう.
Re: どうですかね・・・?
山本明 さんのレス (2005/05/27(Fri) 12:31)
>kouさんへ
スラッシュ( / )の使い方が一般的なやり方とあべこべみたいです. 本来,分数は (分子) ―――― (分母) のように表しますね.だけどこれだと3行に渡ってしまって,見やすいけど書きにくいんですよ.だから分母と分子を分ける真ん中の棒線の代わりに,スラッシュを使います.そのとき,斜め線の上側に分子,下側に分母を持っていきます. つまり,「(分子)/(分母)」と書くのが一般的なやり方です.頭を少し左に傾けて眺めれば,これが分数に見えませんか…??
kouさんが書いた「2/gt × t」というのは, gt ―――― ×t 2 ということですね??だとしたら,それで正解です.
速度と時間のグラフを書いて,そのグラフで囲まれる部分の面積が移動距離になるって指摘は,すでにGoodluckさんがされてるので,私からはそれらと関係ないコメントを.ちょっとこれまでの話の流れからは脱線するので,軽く読み流してみてください.
物理,特に力学ってのは,ある力が働いたときに物がどんな動きをするか予測するという学問分野です.
その際,根幹にしているルールというのがあります.それは「力がかかったら,その方向に速度が増す」ということです.
このルールに従うとすると,こんな動きをしそうだぞ…と予測して,その予測結果と実験事実とを見比べて,よく一致するかどうかを確認する.…これまでに確認したところでは,上記ルールに従ってると考えて予測すると,実験ときちん一致するようだ.ならば上記のルールを出発地点にして,いろいろ考えてみよう.――と,そんな考えで出来上がっています.
「力がかかったら,その方向に速度が増す」ってのを式で書けば, 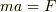 という形になるんですが,式よりも意味合いを覚える方が大事ですね.
という形になるんですが,式よりも意味合いを覚える方が大事ですね.
はじめに書かれていた“隣の屋根まで飛び移る”という問題では,飛んでいる最中にどんな力がかかりそうかなぁ…って予想をしてみましょう.
空気抵抗がないとしたら,かかるのは重力だけです. だから真横に飛び出していたとしても,重力のかかる方向(下方向)への速度はどんどん増していきます.だけど横方向の速度に関しては,重力の影響はないので,ずっと同じ速度で動き続けることになります. 横方向には等速度,縦方向には重力による等加速度の運動をすることになるでしょう.こういう動きの軌跡を「放物線」と呼んでいます.
もし空気抵抗があるとすると,もうちょっと複雑になります.今度は横方向に対しても,動きを妨げる力がかかることになりますね.(縦方向に対しても,動きを妨げる力がかかります) 空気抵抗は,動いている物体の速さが早いほど強くかかると考えられています. そのため,横方向の空気抵抗は飛び出した直後が一番強くて,減速も激しくなります.空気抵抗のせいで減速すると,それにつれて空気抵抗も弱くなります.とはいえ,動いている限り空気抵抗はあるだろうから,いずれは速度が0になるでしょう. 縦方向は,はじめは速度なし=抵抗なしだけど,重力によって速度が増すほどに抵抗も強くなり,いずれ重力と空気抵抗がつりあうくらいの速度に達したら,縦方向の速度はそれ以上変化しない(←力がつり合っているから)ということになります. 空気抵抗がある場合,横方向には減速していずれ止まり,縦方向にはどんどん加速するけど一定の速度でそれ以上速度は変化しなくなる…という動きをしそうです.放物線とはちょっと違った動きになりそうですね.
そういう動きのイメージができるようになると,数式をいじるだけより面白くなるんじゃないかと思います. 大事なのは「力が掛かれば,その方向に速度が変化する」ということ.それと同じことだけど「力が掛かっていなければ,その方向については,速度は変化しない」ということです.
ちなみに空気抵抗がある場合は,高校の物理の範囲ではありません.なので「よくわからないなぁ!」と思っても,まあそんなものかと思って眺めててください.いずれこういう現象についても,式を書いていじれるようになります.
Re: どうですかね・・・?
やかん さんのレス (2005/05/27(Fri) 16:13)
kouさん>
山本明さんがおっしゃられたように
m/s= 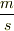 ですよー! :)
斜線の分数を横棒の分数に見るときは,頭は必ず教わった通り,左に傾けて見て下さいね(右に傾けるより楽でしょ!) (^^;
ですよー! :)
斜線の分数を横棒の分数に見るときは,頭は必ず教わった通り,左に傾けて見て下さいね(右に傾けるより楽でしょ!) (^^;
だから
s/m ÷ s = s/m × s/1 = s^2/mではなくて,
m/s ÷ s = m/s x 1/s = m/s^2 ( 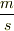 ÷
÷  =
= 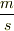 x
x 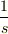 =
= 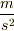 )ですよね.
)ですよね.
>そして,距離を出す式は,2/gt × tですかね?
これも山本さんが教えてくださったように
書き方は2/gtではなくてgt/2ですから
gt/2 x t = 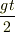 x
x  =
= 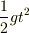 で正解ですね.そうすると,この落ちた距離が10mになるわけですが,
で正解ですね.そうすると,この落ちた距離が10mになるわけですが,
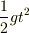 =10とおいて,t=のかたちにgを入れたまま,変形できますか?
=10とおいて,t=のかたちにgを入れたまま,変形できますか?
みなさんに優しく教えていただき本当に感謝しています
kou さんのレス (2005/05/27(Fri) 17:24)
みなさんこんにちは.
Goodluckさん 分数がんばります!
山本明さん ありがとうございます.本当に分数が苦手なもので・・・ これからは気をつけます.左,左・・・
やかんさん t = の形にすればいいのですよね.
また見づらくて申し訳ございません.
まず,1/2 を消すために両辺2倍
2 × 1/2 gt^2 =10 × 2
gt^2 = 20
そして,gを消すために両辺を1/gで割る
1/g ÷ gt^2 = 20 ÷ 1/g
t^2 = 20/g
そして2乗をなくすために,20/gの2乗を求める ___ t =√20/g
なんか違う気がするのですが・・・違いますよね?;
Re: みなさんに優しく教えていただき本当に感謝しています
やかん さんのレス (2005/05/27(Fri) 18:17)
おお,頑張ってる,頑張ってる!結構,いい線いってるのですが,
>そして,gを消すために両辺を1/gで割る
1/g ÷ gt^2 = 20 ÷ 1/g
が違うと思います.”両辺を1/gで割る”ではなくて,
”gで割る”か,”1/gをかける”,のどちらかですね.
数字を例に出すと,”9で割る”と”1/9(= 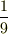 )をかける”が,同じなのと一緒です.それで確かに
t^2 = 20/g
になりますね.
でも
>そして2乗をなくすために,20/gの2乗を求める
これは”2乗を求める”,ではなくて”平方根を求める”ですね.
それで確かに
)をかける”が,同じなのと一緒です.それで確かに
t^2 = 20/g
になりますね.
でも
>そして2乗をなくすために,20/gの2乗を求める
これは”2乗を求める”,ではなくて”平方根を求める”ですね.
それで確かに
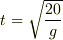 になりますね.
さてかかる時間は
になりますね.
さてかかる時間は  で,距離は20m,
”み・は・じ”でいくと,”は”はどう書けるでしょう?
書けたら,上でせっかく出した,
で,距離は20m,
”み・は・じ”でいくと,”は”はどう書けるでしょう?
書けたら,上でせっかく出した, 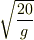 を
を  に当てはめて(代入して)みましょう.どうですか?
に当てはめて(代入して)みましょう.どうですか?
Re: みなさんに優しく教えていただき本当に感謝しています
kou さんのレス (2005/05/27(Fri) 18:30)
やかんさん
>”gで割る”か,”1/gをかける”,のどちらかですね よく考えてみたらそうでした.でも一応合ってるのですよね?だから暖かく見守っください(笑
>さてかかる時間はtで,距離は20m, ”み・は・じ”でいくと,”は”はどう書けるでしょう? 20/tですか?
>当てはめて(代入して)みましょう.どうですか? どの式に当てはめるのですか? 質問ばかりですいません.
Re: みなさんに優しく教えていただき本当に感謝しています
崎間 さんのレス (2005/05/27(Fri) 19:27)
> ”み・は・じ”でいくと,”は”はどう書けるでしょう? > 20/tですか?
そうです ;)
> >当てはめて(代入して)みましょう.どうですか? > どの式に当てはめるのですか? > 質問ばかりですいません.
求めたいのは,速さですね.その速さを  という記号でかくと,上にkouさんがかいた答えから
という記号でかくと,上にkouさんがかいた答えから
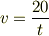
となります.この  に,
に, 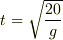 を代入します.すると,それが求める答えです.
を代入します.すると,それが求める答えです.
Re: みなさんに優しく教えていただき本当に感謝しています
kou さんのレス (2005/05/27(Fri) 20:58)
崎間さんこんばんは.
難しいですね・・・ __ v = 20/√20/g
これだけじゃ終わりではないですよね? 何かヒントを出してもらえると嬉しいです. お願いします.
Re: みなさんに優しく教えていただき本当に感謝しています
やかん さんのレス (2005/05/27(Fri) 22:00)
おおっ,いいぞ,いいぞ.
崎間さんじゃないけど,ヒント・・・.
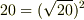 ですよね.
そいでもって
ですよね.
そいでもって 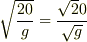 です.
あと,
です.
あと, 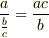 ですよね.
これでどーでしょーか? :)
ですよね.
これでどーでしょーか? :)
Re: みなさんに優しく教えていただき本当に感謝しています
やかん さんのレス (2005/05/28(Sat) 11:02)
おお,合ってます,合ってますよー! ルート記号の中身をまとめられますか?
(^▽^)こんにちは
力 さんのレス (2005/05/28(Sat) 15:10)
(^▽^)こんにちはがんばってますね.物理は興味があるけど勉強不足の力です.kouさんに一番近いのは私だと思う.よろしく! √4*√9=6 √(4*9)=6なのであってるけど
2√5gはパソコン上では紛らわしいです.(2√(5*g)と(2√5)*g) ので2√(5g)と書いておこうかな?
Re: (^▽^)こんにちは
kou さんのレス (2005/05/29(Sun) 07:16)
力さんおはようございます.
確かに,よく考えたら紛らわしいですね.ご指摘ありがとうございます. これからもよろしくお願いします.
やかんさん 返信待ってます.
Re: (^▽^)こんにちは
山本明 さんのレス (2005/05/29(Sun) 17:59)
こんにちは,山本です. やかんさんじゃないけど,コメント付けさせてください.
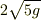 でバッチリですね.
でバッチリですね.
いままでなにをやってたか,思い出してみましょう.「高さ15mの位置から飛び出して,20m先の高さ5mの位置に飛び移るために,どれだけの速さで飛び出せばいいのか」ってことを考えていたのでした.
そのためにまず「高さ15mから高さ5mの位置まで落ちるのは何秒かかるか」を計算しました.それが 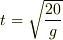 [秒]でした.落ちていくときには,どんどん速度が変化していくってことに注意しながら,計算した結果ですね.
そして,その落下する時間中に20m先まで移動できればいいということなので,「
[秒]でした.落ちていくときには,どんどん速度が変化していくってことに注意しながら,計算した結果ですね.
そして,その落下する時間中に20m先まで移動できればいいということなので,「 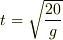 秒間に20メートル進むために必要な速さは…」と計算して出てきたのが,
秒間に20メートル進むために必要な速さは…」と計算して出てきたのが, 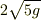 という値.
これの単位は,メートルを秒で割っているので,メートル毎秒ですね.つまり秒速.これはこれで,もう「どれだけの速さで飛び出せばいいのか?」という疑問の答えになっていますよ.
もし時速で求めたいならば,もう少し計算してみましょう.(…できそうですか??)
という値.
これの単位は,メートルを秒で割っているので,メートル毎秒ですね.つまり秒速.これはこれで,もう「どれだけの速さで飛び出せばいいのか?」という疑問の答えになっていますよ.
もし時速で求めたいならば,もう少し計算してみましょう.(…できそうですか??)
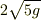 と見ても,どれくらいの速さかイメージできない…ならば,最後に
と見ても,どれくらいの速さかイメージできない…ならば,最後に  に具体的な数字を代入してみましょう.
に具体的な数字を代入してみましょう.
 の値はすでに測定した結果があって,約 9.8 [m/s^2]という数字だとわかっています.そこで
の値はすでに測定した結果があって,約 9.8 [m/s^2]という数字だとわかっています.そこで  のところに 9.8 という数字を代入してみましょう.
なんだったら,9.8 はおよそ 10 だと思って,
のところに 9.8 という数字を代入してみましょう.
なんだったら,9.8 はおよそ 10 だと思って, 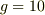 を代入して計算しても,およその値として悪くないと思います.
平方根の値を手計算で求めるのは大変なので,そこは電卓を使っちゃいましょう.
を代入して計算しても,およその値として悪くないと思います.
平方根の値を手計算で求めるのは大変なので,そこは電卓を使っちゃいましょう.
Re: これでいいですかね?
山本明 さんのレス (2005/05/29(Sun) 19:45)
あ,ホントだ.9.8を代入した方が,平方根が外しやすいですね (^^; .
おっしゃる通り, 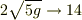
![[m/s]](http://hooktail.maxwell.jp/bbslog/3372272ffdcb72b1eb66a919839dfcf0.png) です.
これだけの速さで飛び出せば,20m先で10m下の屋根に飛び移れるというわけです. :)
です.
これだけの速さで飛び出せば,20m先で10m下の屋根に飛び移れるというわけです. :)
1秒間に14m進む速さというと…かなりの速さですね. 100メートル走の世界記録が10秒をちょっと切るくらいですよね.すると人間の力だけで,秒速14メートルで飛び出すのはかなり難しそうですね.
Re: これでいいですかね?
kou さんのレス (2005/05/29(Sun) 20:02)
やっと解決できました. でも,もう一度見直さないとやり方すら忘れてるかもしれません・・・ この次の段階というのもあるんでしょうか?
Re: これでいいですかね?
山本明 さんのレス (2005/05/29(Sun) 21:07)
そうですね.もう一度ゆっくり見直してみると,いい勉強になると思います.
この次の段階というと,どんなものがあるかなぁ…. 例えば,いまの場合は真横に飛び出すってことを考えてみたけど,少し上方へ飛び出すと,もうちょっと飛距離が稼げそう.だから少し角度を付けて飛んでみる…とかなら,考えやすいかもしれません.
Re: これでいいですかね?
やかん さんのレス (2005/05/30(Mon) 13:19)
kouさん,こんにちは!昨日は掲示板見れなくてすみません!
正答出たようで本当に良かったですね!一生懸命考えて
出された解答だから,嬉しさもひとしおなのでは? :)
山本明さんや,他の方にも,とてもわかりやすくて,ためになる
レスをいただいて良かったですね.あと私が思ったのは,
もう一度この問題を白い紙に最初から書いて,解けるか(誰かに説明しようとしたらできるか)を確かめたり,高度差を 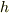 ,距離を
,距離を 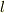 とか
文字で置き換えてもう一度式をたてたりとか,してみたらどうでしょう?
文字が増えるだけで,ぐっと難しく感じるかもしれませんが,慣れるためには
いいかと思います.レスでご指摘されたように,グラフを書いてみるとか・・・.
このスレッドを何回も最初から読みなおされると,知識がもっと定着するかもしれませんね.頑張って下さいねー,応援してますよー(^-^)/
とか
文字で置き換えてもう一度式をたてたりとか,してみたらどうでしょう?
文字が増えるだけで,ぐっと難しく感じるかもしれませんが,慣れるためには
いいかと思います.レスでご指摘されたように,グラフを書いてみるとか・・・.
このスレッドを何回も最初から読みなおされると,知識がもっと定着するかもしれませんね.頑張って下さいねー,応援してますよー(^-^)/
Re: これでいいですかね?
通りすがりです. さんのレス (2005/05/30(Mon) 20:24)
14[m/s]に,3.6を掛け算すると, 50.4[km/hour]になります.
時速50.4kmよりも速く走れば飛び移れそうですね.
kouさん,これからも物理を楽しんでみてね.
Re: これでいいですかね?
kou さんのレス (2005/05/30(Mon) 21:02)
みなさん本当にありがとうございました. これで力学を大分理解できました. これからも質問をすることがあると思いますので,そのときはまたよろしくお願いします.