物理難しいです;;
物理難しいです;;
みう さんの書込 (2005/05/21(Sat) 16:59)
高2生のみうです「2.0m/sの速さで流れる川を船で横切るための船首を川岸にそった上流の向きに対して60°の方向へ向けた.この船の,川の流れがないときの速さが4.0m/sのとき,岸から見た船の速度の向きと大きさV{m/s}を求めよ」って問題なのですが・・ 上流の向きに対して60°の方向へ向けるの意味がわかりません.教えていただけないでしょうか??あとこれはv=?r/?tの公式をつかうのでしょうか??
Re: 物理難しいです;;
tomo さんのレス (2005/05/21(Sat) 19:21)
みうさん,こんにちは.tomo@M2です.
船の先頭の部分(船首)をA,一番うしろの部分をBとしますね. 川岸で船が先頭の部分Aを上流に向けてとまっているとします.
<pre> (川岸) ――――――――――――――――――――
(上流) (下流)
A---B ―――――――――――――――――――― (川岸) </pre>
という状態です.Bの方を固定して,Aを反対側の川岸の方に向けてまたとめます. <pre> (川岸) ――――――――――――――――――――
(上流) (下流) A A' B ―――――――――――――――――――― (川岸) </pre>
最初AがあったところをA'として表示しています. ここで,∠A'BA=60°となった状態が, 「川岸にそった上流の向きに対して60°の方向へ向けた」状態だと思います.
> これはv=?r/?tの公式をつかうのでしょうか?
う〜ん…この問題には距離(?r)の情報も時間(?t)の情報もないですから, その公式を使おうとしてもちょっと難しいのではないでしょうか?
ありがとうございます!!
みう さんのレス (2005/05/21(Sat) 20:16)
すごくわかりやすく図までつけていただきありがとうございます!!! それで,岸から見た速度の向きとゆうのはAがわに近いほうの岸なんですか?? それについての説明が問題文にないので・・.
もう1つ
みう さんのレス (2005/05/21(Sat) 20:18)
距離と時間情報も
もう1つすいません.
みう さんのレス (2005/05/21(Sat) 20:21)
さっきの記事は間違えました,すいません..時間も距離もわからないのにVはでるんでしょうか??私の知ってる中の公式はそれしかなくて・・どうやってもとめていいかわかりません.
Re: もう1つすいません.
tomo さんのレス (2005/05/21(Sat) 21:10)
こんばんは.
「岸から見た」というのは,上に示した「(川岸)」というところから見たという意味ですね. 川の中にいて流されながら船を見ている人と,川岸で船を見ている人では, 船の動いている方向や速さが違ったように見えてしまうので, 「岸から見た」というように条件がつけられているのです.
> 時間も距離もわからないのにVはでるんでしょうか??私の知ってる中の公式はそれしかなくて・・どうやってもとめていいかわかりません.
この問題で聞かれていることを日常生活の例で考えてみると以下のような感じです. みうさんは,横断歩道を南から北に向かってわたろうとしています. その時,西から東へ2[m/s]の風が吹いてきていました. 風に流されることを考えて,西から北に向かって60°の方向(上の図に示した方向)に体を向けて4[m/s]で歩きました. 結果として,どちらの方向にどれだけの速さで歩いたことになりますか. (まぁ2[m/s]程度の風で人間は流されないんですが,流されるものとして.)
要するに,速度ベクトルを合成する問題です. 上に挙げた例で余計分かりにくいよ!!ってなってしまったらごめんなさいね.
Re: もう1つすいません.
Joh さんのレス (2005/05/21(Sat) 21:41)
たしかに,混乱しますね.
岸,川の水,ボートというのがあって, 水は流れているし,ボートは水に対して動いているし, ということなんですねぇ.
船は,舳先へ4.0m/sで進む能力があるんですね. で,水は流れています.岸からみると,水とボートの 動きを合成したようなものが見えるんでしょうか.
順番に頭を整理してみれば,きっと分かります.
ありがとうございます!!
みう さんのレス (2005/05/22(Sun) 11:11)
みなさん説明がすごくわかりやすいですね.ありがとうございます!! 私は三角比を用いて計算しようと思いました.
| | | 4.0m Xm | | | 60° (  ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
2.0m
直角三角形ができて比が1:2:√3になるので xは2√3だと思いました. なのでV{m/s}は2√3m/sかなと思ったのですが 答えを見ると3.5m/sなのです. 2√3をなぜ3.5に直すのでしょうか??
Re: ありがとうございます!!
やかん さんのレス (2005/05/22(Sun) 14:10)
みうさん,はじめまして!
>2√3をなぜ3.5に直すのでしょうか??
多分,これが数学の問題ではなくて,物理の問題だからではないでしょうか?
問題文を見ると,2.0とか,4.0とか,有効数字2けただから,答えも
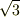 に1.732・・・(ヒトナミニオゴレヤ)を代入して
桁数をそろえたのでは?
に1.732・・・(ヒトナミニオゴレヤ)を代入して
桁数をそろえたのでは?
Re: ありがとうございます!!
Joh さんのレス (2005/05/22(Sun) 17:54)
確かに,小数で書くのはよくわかりませんが, どっかに,やかんさんが書かれたように, 有効数字ナントカで答えを書けとか,そういう 指示があるのではないでしょうか.
指示がなければ, 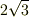 で
いいと思います.
で
いいと思います.
私は,無理数を小数で書くのは好きじゃないですけど, 具体的な現象をイメージするには,こういうのもいい んですかねぇ.
Re: ありがとうございます!!
feder さんのレス (2005/05/22(Sun) 18:42)
みうさん,はじめまして.
やはり,やかんさんが指摘されているように,有効数字2桁にそろえるために無理数を少数に書き直したのでは.
問題文に具体的に数値が与えられているなら,出した答えの有効数字も考察の対象になると思いますし. 2√3のままじゃあ,有効数字の情報がないため,この数値はどこまで信用してよいのか?というのが分かりませんよね.
ちなみに,文字式をいじくって答えを出す場合,有効数字を考える必要がないため,√3ももちろんそのままで答えます.