よろしくお願いします
よろしくお願いします
翔 さんの書込 (2005/05/19(Thu) 22:27)
大学一年生の翔です.よろしくお願いします. 同じ周期T,同じ振幅Aで単振動している2つのバネがある.ある時刻での変位が一方は1/2で,他方は−1A/√2であり,ともにつりあいの位置に向かっていた.位相差をもとめよ. 答えもわからないし,T軸のグラフの作り方もわかりません.お願いします.
Re: よろしくお願いします
やかん さんのレス (2005/05/20(Fri) 18:26)
翔さん,はじめまして!私は教えられるわけではないですが,一緒に考えませんか?
単振動だと変位  ,周期
,周期 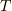 ,振幅
,振幅 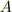 ,時刻を
,時刻を  ,位相差を
,位相差を  として,変位2つで2つの式ができますでしょうか?それと変位は
として,変位2つで2つの式ができますでしょうか?それと変位は 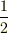 と,
と, 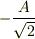 (片方にだけ
(片方にだけ 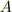 がついている)でよろしいでしょうか?
がついている)でよろしいでしょうか?
Re: よろしくお願いします
翔 さんのレス (2005/05/20(Fri) 21:37)
すいません.左の変位はA/2でした.右はそれでいいです.変位が2つでも時刻が違えばこの2つの変位を通るから1つの式ができると思うんですがどうですか?
Re: よろしくお願いします
やかん さんのレス (2005/05/21(Sat) 13:36)
この問題の場合,”ある時刻”だから,両方のバネの変位を表す式中の  は同じ値ですよね.周期も振幅も同じだから,位相の違いだけで
変位の値の違いが出てるわけですが,両方のバネとも単振動だから三角関数を含む同じ式でかけて,変位と位相差(
は同じ値ですよね.周期も振幅も同じだから,位相の違いだけで
変位の値の違いが出てるわけですが,両方のバネとも単振動だから三角関数を含む同じ式でかけて,変位と位相差(  )の違いがあるだけですよね?
単振動の式ご存知ですか?(私も忘れていたので急いでネットで調べてみました(^^;)
)の違いがあるだけですよね?
単振動の式ご存知ですか?(私も忘れていたので急いでネットで調べてみました(^^;)
Re: よろしくお願いします
tomo さんのレス (2005/05/21(Sat) 21:50)
翔さん,こんばんは.tomo@M2です.
位相差を求めよという問題ですけど,位相って分かりますか? 時刻をt,周期をTとして図を描いてみます. 本来は左右だけの動きですが,重ねて書くと分かりにくいので, 時間が経過したものをどんどん下に書いて示しています.
(図の意味が分かりにくかったらごめんなさい.)
<pre> /| /|-------------○(つり合いの位置:t=0…右に動いています) /| |← A →| /|---------------------○(t=T/4…一瞬止まりました) /| /|-------------○(t=T/2…左に動いています) /| |← A →| /|------○(t=3T/4一瞬止まりました) /| /|-------------○(つり合いの位置:t=T…右に動いています) /| </pre>
つり合いの位置にいた時をt=0とすると, そこから振幅A運動した時,つりあいに位置に戻ってきた時, さらに振幅A運動した時の時刻が,上に示したようになることは分かりますか?
さて,t=0の時の位相を0として,上に書いた残りの4つの場合の位相がいくつになるか,分かりますか.
<pre> →…こちらを+に取ります. /| /|-------------○(つり合いの位置:t=0…右に動いています) /| |← A →| /|---------------------○(t=T/4…一瞬止まりました) /| |A/2| /|-----------------●(つり合いの位置に向かって動いています) /| /|-------------○(t=T/2…左に動いています) /| |← A →| /|------○(t=3T/4一瞬止まりました) /| | A/√2| /|--------●(つり合いの位置に向かって動いています) /| /|-------------○(つり合いの位置:t=T…右に動いています) /| </pre>
●で示したところが問われているところですよね. それぞれの位相と,位相差,求められますか?
Re: よろしくお願いします
tomo さんのレス (2005/05/21(Sat) 21:57)
こんばんは.再びtomoです.
すみません,2つのばねがあるという設定なのに,1つのばねで示してしまいました. 分かりにくかったらお詫びします.