マクローリン展開

きすけさんの書込 (2005/05/12(Thu) 00:42)

大学の授業で次のような問題が出ました．次の関数をマクローリン展開し４次の項まで求めよ． expＸ√(１-Ｘ2乗) わかってもらえるかなぁ(^_^;) で，答えは１＋Ｘ＋Ｘ2乗/２＋Ｘ3乗/２＋１３Ｘ4乗/２４らしいんですが，何度やってみてもなりません． f(Ｘ)＝expＸ

＝１＋Ｘ＋Ｘ2乗/２!＋Ｘ3乗/３!＋・・・＋Ｘn乗/n!＋・・・

g(Ｘ)＝√(１−Ｘ2乗): ＝１−Ｘ2乗/２＋Ｘ4乗/８＋・・・
となり（ f(Ｘ)，g(Ｘ)ともにマクローリン展開しました．）: f(Ｘ)g(Ｘ)＝expＸ√(１-Ｘ2乗)

なので計算すると・・・あれれ？？？という状況です．ご意見よろしくお願いします．

Re: マクローリン展開

Joh さんのレス (2005/05/12(Thu) 01:42)

＞わかってもらえるかなぁ(^_^;)

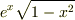むむ．問題の関数は $\exp [x \sqrt{(1-x^2)}]$ ですか？それとも $e^x \sqrt{1-x^2}$ でしょうか．

できれば，掲示板の使い方を読んで，数式でお願いします．

Re: マクローリン展開

きすけさんのレス (2005/05/12(Thu) 20:04)

申し訳ないですｍ(__)ｍ数式で載せたいのですが，どうやればいいのかわかりません．載せたかったのは後者の式です．どう表現すればいいか悩み，先生がｆ(Ｘ)＝expＸ＝ex乗と書いていたのを思い出し，載せたのですが・・・．間違っていたのならすみません． expＸは何を表すものなんですか？いろいろほんとすみません．

Re: マクローリン展開

やかんさんのレス (2005/05/12(Thu) 22:41)

きすけさんはじめまして！

確かにこれ，Johさんがおっしゃるように数式じゃないときついかもですね．（解けるわけじゃないのにレス書いてすみません）上の

http://hooktail.maxwell.jp/yybbs/texuse.html

に使い方出てますよ．全部覚えなくても全部半角で＜ｔｅｘ＞〜＜／ｔｅｘ＞の〜に書きたいもの書けばできちゃいますよ（中身はJohさんの数式部分にポインタあてれば，黄色地に出てきます）．指数は＾だし・・．私でもできるんだから大丈夫ですよ・・・．expXって 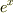e^x の事ですか？違うことお答えしてたらすみません．

Re: マクローリン展開

Joh さんのレス (2005/05/13(Fri) 09:26)

とをそれぞれ別々に

マクローリン展開して，最後に掛け合わせるという手順自体は正しいんでしょうか．

Re: マクローリン展開

tomo@研究室さんのレス (2005/05/13(Fri) 17:06)

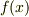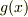> f(x) と g(x) をそれぞれ別々に > マクローリン展開して，最後に掛け合わせるという手順自体

正しくないですよね．

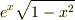$e^x\sqrt{1-x^2}$ について普通に計算してみましたが，きすけさんがNo.5146に書かれた答えとは合いませんでした…．

Re: マクローリン展開

きすけさんのレス (2005/05/13(Fri) 23:53)

johさん，やかんさん，tomoさんご意見ありがとうございます．結局すべてまとめてマクローリン展開するしかないのでしょうか？僕もやろうとして，２回微分ぐらいですごい式になって挫折してしまいました．根気が足りないのかなぁ．最近毎週毎日未解決の課題が増えてほんと進級できるか心配です．次から載せるときは数式で載せるようにがんばります．

Re: マクローリン展開

おこめさんのレス (2005/05/14(Sat) 00:42)

きすけさんはじめまして．マクローリン展開は定義に従ってやるしかないですが，ここまでの計算を再利用すれば案外，簡単に計算できると思いますよ．別々のマクローリン展開がもとまっているのであれば，すでに

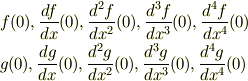
$&f(0),\frac{df}{dx}(0),\frac{d^{2}f}{dx^{2}}(0),\frac{d^{3}f}{dx^{3}}(0),\frac{d^{4}f}{dx^{4}}(0)\\&g(0),\frac{dg}{dx}(0),\frac{d^{2}g}{dx^{2}}(0),\frac{d^{3}g}{dx^{3}}(0),\frac{d^{4}g}{dx^{4}}(0)$

は既知のはずです．そこで，関数の微分の公式を使えば

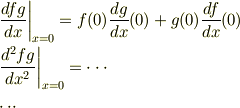
$&\left.\frac{d fg}{dx}\right|_{x=0} = f(0)\frac{dg}{dx}(0) + g(0)\frac{df}{dx}(0)\\&\left.\frac{d^{2}fg}{dx^{2}}\right|_{x=0} = \cdot\cdot\cdot\\&\cdot\cdot\cdot$

と難しい計算無しでも（書くのは省略してしまいましたが）全てもとまると思います．

Re: マクローリン展開

tomo さんのレス (2005/05/14(Sat) 02:19)

きすけさん，Johさん，おこめさん，こんばんは．tomo@M2です．上の書き込みであいさつを忘れました．すみません．

> 僕もやろうとして，２回微分ぐらいですごい式になって挫折してしまいました．
> 根気が足りないのかなぁ．

マクローリン展開に限らず，物理数学はある程度の計算量を覚悟した方が良いかもしれません．まともにやったら2階微分あたりでしんどくなるもの分かります．少し計算の仕方を工夫してみませんか．計算量が多くなりそうだったら，一気にやろうとせずに，少しずつ分けてやると良いですよ．今回の場合，おこめさんが示してくれたような方法もありますし，以下のような方法もあります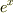． e^x を含んだ関数では，少し工夫すると計算量が少なくなったり見やすくなったりすることがあります．

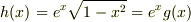$h(x)=e^x\sqrt{1-x^2}=e^xg(x)$ とおきます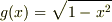． $g(x)=\sqrt{1-x^2}$ ですね．

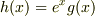
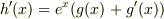
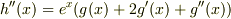
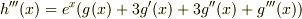
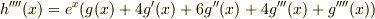
h(x)=e^xg(x) h'(x)=e^x(g(x)+g'(x)) h''(x)=e^x(g(x)+2g'(x)+g''(x)) h'''(x)=e^x(g(x)+3g'(x)+3g''(x)+g'''(x)) h''''(x)=e^x(g(x)+4g'(x)+6g''(x)+4g'''(x)+g''''(x))

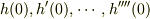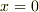ほしいのは， $h(0), h'(0), \cdots , h''''(0)$ ですから，上の5つの式に x=0 を代入して計算します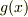． g(x) のマクローリン展開をした際に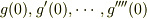， $g(0), g'(0), \cdots , g''''(0)$ はもう計算してありますよね．あとは上の5つの値をマクローリン展開の式に代入するだけです．（かえって分かりにくい方法だったらごめんなさい．）

がんばってください．

Re: マクローリン展開

feder さんのレス (2005/05/14(Sat) 14:38)

こんにちは．ちょっと気になったので書き込ませていただきます．よろしくお願いします．

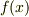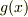＞ f(x) と g(x) をそれぞれ別々にマクローリン展開して，最後に掛け合わせるという手順自体

正しいんじゃないですか？

それを数学的に示すのは難しいかわかりませんが，少なくとも，2次までの展開を考えるにあたっては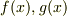， f(x),g(x) をそれぞれ別々に展開してもよいことは簡単に確かめられます．

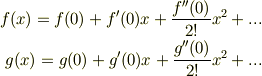
$f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+... \\g(x)=g(0)+g'(0)x+\frac{g''(0)}{2!}x^2+...$

また，

f(x)g(x)=f(0)g(0)+[f(0)g'(0)+f'(0)g(0)]x+[f''(0)g(0)+2f'(0)g'(0)+f(0)g''(0)]x^2/2+...

となりますが，これは上の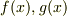， f(x),g(x) を個別に展開してかけあわせたものと等しいです．

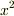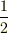しかし，きすけさんの持っている解答では， x^2 の係数が $\frac{1}{2}$ となっていますが，この方法ではゼロになってしまいます．よって，これは，きすけさんの用意されている解答が間違っているのでは？

Re: マクローリン展開

feder さんのレス (2005/05/14(Sat) 15:23)

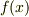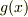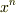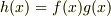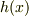ちょっと試してみたところ， f(x) と g(x) を個別に展開して，これらをかけあわせたものの x^n の係数が， h(x)=f(x)g(x) として， h(x) をそのまま展開したもののそれと等しくなることは容易に示せそうです．面倒なのでここには書けませんが（苦笑）

Re: マクローリン展開

おこめさんのレス (2005/05/14(Sat) 15:31)

計算してみましたが，fとgの展開したものを掛け合わせても合っていそうですね (^^; （近似の精度が違うので，切り捨てる必要があると思いますが）

Re: マクローリン展開

tomo さんのレス (2005/05/14(Sat) 15:37)

こんにちは．

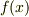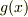＃tomo@No.5159 >> f(x) と g(x) をそれぞれ別々に >> マクローリン展開して，最後に掛け合わせるという手順自体 > > 正しくないですよね．

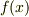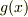＃federさん@No.5169 >> f(x) と g(x) をそれぞれ別々に >> マクローリン展開して，最後に掛け合わせるという手順自体 > > 正しいんじゃないですか？

計算せずに直感で書いたので，私の方が違っているかもしれません．無責任な書き込みですみません．

ここまで来れば，きすけさんも計算できるでしょうか． federさんがおっしゃっているように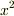， x^2 の項は係数がになるので落ちます．お手元の解答は気にしないでやってみてください．

> federさん@No.5169へ

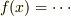
「それぞれマクローリン展開してからかけても正しい」という書き込み，ありがとうございました．そのレスの途中に書かれている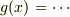， $f(x)=\cdots$ $g(x)=\cdots$ のところで，各項の累乗が抜けてしまっています．もしパスワードを入力されているようでしたら，修正ができるので，きすけさんのためにも修正をお願いしますm(_ _)m．

Re: マクローリン展開

feder さんのレス (2005/05/14(Sat) 15:43)

ところで，そうすると，きすけさんの用意した答えはどういう関数を展開したものなのでしょうね．問題の関数に近い別の関数でいろいろ試してみたけれど，あの答えに合う関数が見つからず．うむむ．．

Re: マクローリン展開

おこめさんのレス (2005/05/14(Sat) 15:56)

>きすけさんへこの公式はとりあえずライプニッツの公式(これも証明したければ数学的帰納法あたりを使えば良いと思います)を使えば示せると思います :)

Re: マクローリン展開

tomo さんのレス (2005/05/14(Sat) 15:59)

こんにちは．

> きすけさんの用意した答えはどういう関数を展開したものなのでしょうね．

ん〜．きすけさんもNo.5146で，

> で，答えは
> ・・・
> <b>らしい</b>んです

と書かれているので，解答の出典が謎なんですよね．「質問する方へ」のところに，「解答を書く場合はその出典も明記すること」という注意書きを入れた方が良いのかもしれません．先生が黒板に書いたものなのか，本から取ってきたものなのか，はたまた友達に聞いたのか…etc.．

Re: マクローリン展開

feder さんのレス (2005/05/14(Sat) 16:21)

tomoさん，指摘ありがとうございます．数式直してきました．

Re: マクローリン展開

きすけさんのレス (2005/05/16(Mon) 09:10)

ここ２，３日寝てる時間もないくらい忙しいです．レスできなくてすみません．たくさんのご意見ありがとうございます．

＞きすけさんも計算できる＞係数が０になる

はじめ僕もこの方法で計算してみました．するとやはり０になりました．このやり方だと明らかに模範解答にはなりません．そこで自分のやり方が正しいのかわからず，書き込ませてもらいました．

＞解答の出典が謎

出典は友達が写した黒板の写しです．ちょっと怪しい雰囲気がしますが，二人に聞いて，二人とも同じことを書いているので間違いないと思います．やはり模範解答が間違っているのでしょうか．．．先生に聞いてみたいと思います．

[home] [掲示板] [ページの先頭]