どなたか教えてください.
どなたか教えてください.
めそ さんの書込 (2005/05/06(Fri) 01:35)
今高校3年生です,どうしてもわからない問題があって解ける方がいたら教えてほしいのですが 楕円運動x=Acos(ωt+α),y=Bsin(ωt+β)の軌道を求めよ というものですα,β両方あるので位相が合わないような気がしたり,とにかくよくわかりません.
Re: どなたか教えてください.
おこめ さんのレス (2005/05/06(Fri) 18:56)
こんなので良いですか?
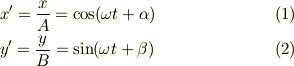
ここで三角関数を分解して(この公式は高校の数学の教科書に載っています)
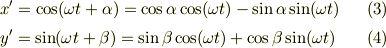
を得ます.  と,
と, 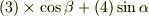 から
から
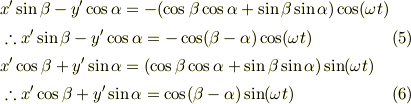
が言えますので 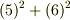 から
から
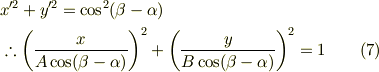
を得ることができるわけです. 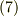 は楕円の方程式そのものなのですが,
は楕円の方程式そのものなのですが,  のときは
のときは 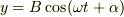 になりますので
になりますので 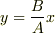 の傾きで単振動する運動をすると思います.では
の傾きで単振動する運動をすると思います.では 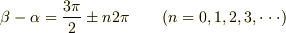 の場合はどうなるでしょうか?
の場合はどうなるでしょうか?
あと余談ですが,リサージュ図形というもっと一般的な関係を図で表したものがあります.
今回の場合は,周波数比1:1の部分です.
リサージュ図形関係でこんなページもあります(COさんのページです).
Re: どなたか教えてください.
やかん さんのレス (2005/05/06(Fri) 19:07)
めそさん,おこめさん,こんにちは. 横から見ていて,問題の難しさと, 解法の見事さに感心してしまいました・・・. こういうのやっぱ大学受験で出るんでしょうかね. もし出たら,私ならひとたまりもないなあ. めそさん,教えていただいて本当に良かったですね :)
Re: どなたか教えてください.
めそ さんのレス (2005/05/06(Fri) 19:48)
おこめさん丁寧に答えていただいてありがとうございます.とても参考になりました.なんとか解かってきましたが,(7)の楕円の方程式以降のところが難しいのでもう少し考えてみたいと思います.
Re: どなたか教えてください.
おこめ さんのレス (2005/05/06(Fri) 20:13)
>やかんさん >こういうのやっぱ大学受験で出るんでしょうかね. どうなんでしょうか.僕も出されたらひとたまりもありません :)
>めそさん
円の方程式から楕円ならば説明することはできそうですが,考えてみるということなので頑張ってください :)
Re: どなたか教えてください.
CO さんのレス (2005/05/06(Fri) 22:00)
から
式になりますか?? (ついでに(5),(6)式が微妙に違うような)
Re: どなたか教えてください.
おこめ さんのレス (2005/05/07(Sat) 00:00)
完全に計算が間違ってますね.COさんありがとうございます,そしてめそさんすみません(まだ見てるかな).ちゃんと紙とペンを使って計算し直したところ次のようになりましたが,確かではないです.
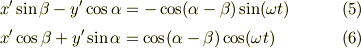
で 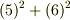 から
から
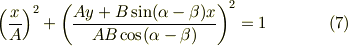
あと変数を 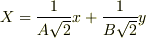 ,
, 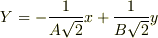 (
( 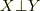 )に変換すると
)に変換すると  と
と  の絡みがとけて
の絡みがとけて
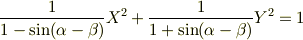
と書けると思います.
Re: どなたか教えてください.
めそ さんのレス (2005/05/07(Sat) 01:54)
もう一度見直してみます,わざわざありがとうございました.
Re: どなたか教えてください.
おこめ さんのレス (2005/05/07(Sat) 05:03)
ほんとどうもすみません.
あと変数変換でもう一つ紹介しておこうと思います.
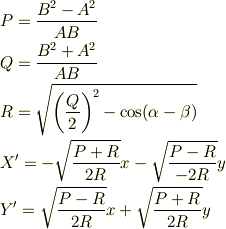
とすると 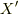 ,
, 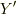 が満たす方程式は次のようになると思います(
が満たす方程式は次のようになると思います( 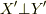 ).
).
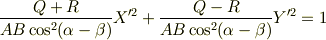
この変換は前とは違って,基底の大きさが1になる様に調節してあります(つもりです).
僕もこの種の問題を解いたことは無いので,間違っていたら教えてください. 何気(無責任)に書き込みをしていましたが,もっとその事をはやく言うべきだったかもしれないです.
Re: どなたか教えてください.
CO さんのレス (2005/05/09(Mon) 17:02)
「二次形式」「回転行列」などがキーワードでしょうか.その辺の記事もあるといいですね. :)