フーリエ級数展開

フーリエ級数展開

hydrangeas さんの書込 (2005/05/04(Wed) 01:27)

初めて投稿させていただきます．今年はめでたく2年に進級できまして(必修の数学系の単位を一つ落としたけど)，"関数解析概論"という授業を履修しておりますが，フーリエ級数展開がさっぱりわからないので，困っています．5/2に下記の課題を出されました． 1.次の関数の周期を求めよ

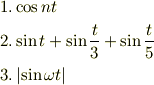
&1. \cos nt&\\&2. \sin t + \sin \frac{t}{3} + \sin \frac{t}{5}&\\&3. \left| \sin \omega t \right|&
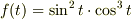  1. f(t) = \sin^{2} t \cdot \cos^{3} t のフーリエ級数を求めよ．

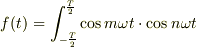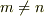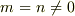他の問題は出来たのですが，この4問がわかりません． 1.1は f(t) = \int_{-\frac{T}{2}}^{\frac{T}{2}} \cos m \omega t \cdot \cos n \omega t とおいて， m \neq n と m = n \neq 0 の場合でそれぞれ，積和の公式若しくは2倍角の公式から導き出せるかな…と． で，

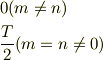
&0 (m \not= n)&\\&\frac{T}{2} (m = n \not= 0)&

と出したのですが，もしかしたら，全く見当違いのことを書いているかもしれないです．

だらだらと長くなってしまって申し訳ありませんが，よろしくおねがいします．

Re: フーリエ級数展開

CO さんのレス (2005/05/05(Thu) 12:24)

hydrangeas さん，こんにちは．

1番は落ち着いて考えればすぐにわかると思いますよ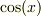． \cos (x) の周期は知っていますよね？ とりあえずグラフを描いてみてはどうでしょう．

2番は積分ができるような形に変形していくとよいと思います．公式を使って，三角関数の次数を下げていくと良いでしょう．

Re: フーリエ級数展開

hydrangeas さんのレス (2005/05/05(Thu) 14:09)

少し間違った方向へ行ってしまっていたようです...

1番はグラフを書けばそれほど難しくはなかったです．

2番もなんとか，積分できる形まで持っていくことが出来ました．

本当にありがとうございました．