初歩的な計算の質問です
初歩的な計算の質問です
おこめ さんの書込 (2005/03/23(Wed) 09:33)
すみません.初歩的な計算が分かりません.良かったら教えていただきたいと思います.
【学年・物理学習の度合い】
学部新3年
【問題の引用元】
詳解力学演習後藤,山本,神吉共編共立出版p52 第2章§5 {1・2}
【どこまでできたか(自分で調べたこと)】
 が
が 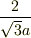 に比べて十分微小な量である場合の計算なのですが次の式の計算が演習書の答えと一致しません.
に比べて十分微小な量である場合の計算なのですが次の式の計算が演習書の答えと一致しません.
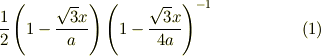
ここでマクローリン展開の1次近似までをとった
![(1 + \alpha x)^{n} \simeq 1 +n(\alpha x) ,[ \alpha x << 1] \tag{2}](http://hooktail.maxwell.jp/bbslog/151bde593beb9e36613988eee2badafa.png)
を用いて
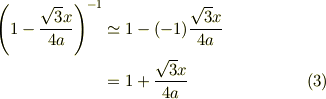
になると思います.すると 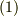 は近似的に次のようになると思います.
は近似的に次のようになると思います.
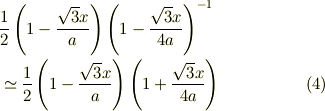
最終的に2次の微少量を無視した近似をとると
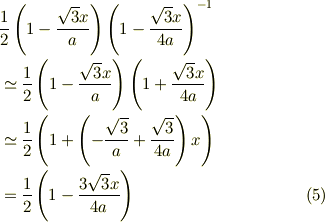
になると思うんです. 【どこが分からないか】 ところが結果は
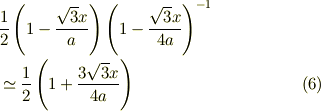
になっています.
公式の確認
おこめ さんのレス (2005/03/23(Wed) 10:03)
念のために近似式の公式を確認しておきました.まず関数を
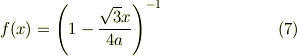
としますとマクローリン展開の一次までとった近似は
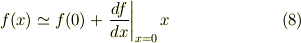
になると思います.まず  を微分すると
を微分すると
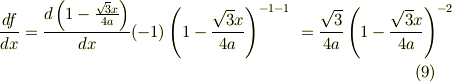
なので近似式は
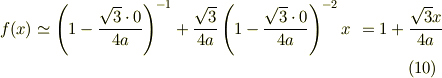
です.これだとどうしても演習書の結果とは一致しません.単なる誤植でしょうか?
Re: 公式の確認
CO さんのレス (2005/03/23(Wed) 16:40)
誤植だと思います :)
Re: 公式の確認
やかん さんのレス (2005/03/23(Wed) 17:40)
おこめさん,COさん,こんにちは. おこめさん,大学院受験されるとの事,頑張って下さいね. かげながら応援しております. (私の大学院時代は,結果的にネズミを大量に死なせてしまった 事が今考えても申し訳ないです (^^;
微分も積分も良くわかってない私が,おこめさんのご質問にレス書くのは
百万年早いとは思いましたが,条件から仮に
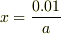 とおき,
仮に
とおき,
仮に 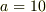 として,電卓で計算してみたのですが
やはりおこめさんの御解答の方が,近似が良いようです.
生意気ですみません・・.
として,電卓で計算してみたのですが
やはりおこめさんの御解答の方が,近似が良いようです.
生意気ですみません・・.
Re: 公式の確認
かつ さんのレス (2005/03/23(Wed) 22:01)
>やかんさん まじめな話,そういう考えに基づく計算は凄く良いと思いますよ ;) 摂動論なんて,言ってみればそういう考えの延長なんですし.
Re: 公式の確認
崎間 さんのレス (2005/03/23(Wed) 22:26)
> >やかんさん > まじめな話,そういう考えに基づく計算は凄く良いと思いますよ ;) > 摂動論なんて,言ってみればそういう考えの延長なんですし.
僕も非常にそう思います! ぱっとみて,やかんさんの方法は思い浮かびませんでしたー (^^; ちなみに僕が一度だけ飼ったハムスターは,冬を越せませんでした……
Re: 公式の確認
おこめ さんのレス (2005/03/24(Thu) 02:30)
みなさんどうもありがとうございます. 微小振動の問題で,その後の計算も間違ったまま進んでいるので「僕の方が間違っているのかな?」とか思ってしまいました. 力学演習91版にして,まだ誤植も多いのですね.たまに図の間違いもあったのですが,答えの間違いを見つけたのは初めてだと思います.
やかんさんの検算方法なら自分の作った近似を簡単に評価できますね.これからは使わせていただきます(多分かんがえることを自分は少し止めていました.).