解析力学

home > 掲示板 >

このページのPDF版

サイトマップ

解析力学

やかんさんの書込 (2005/03/18(Fri) 17:24)

以前こちらで御紹介いただいた書籍”道具としての物理数学”が面白くてわからないところが多いなりにトボトボ読んでいるのですが，どうしてもお聞きしたいところが出てきてしまいました．すごく初歩的な事のようですみません．

解析力学の導入説明で前章で出てきた変分を使って，運動エネルギーＴが少しずれた時を考え，時刻ｔにおけるＴの変分が，

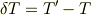
$\delta T=T'-T$

であり，

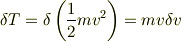
$\delta T=\delta\left(\frac{1}{2}mv^2 \right)=mv \delta v$

と書いてあるのですが，どうして２番目の真中の式から右辺になるのかわかりません．その先続く変形はなんとかわかるのですが・・．お教えいただいてもよろしいでしょうか？

Re: 解析力学

Joh さんのレス (2005/03/18(Fri) 18:28)

変分じゃなくて微分だったとしたらどうでしょう．

Re: 解析力学

やかんさんのレス (2005/03/18(Fri) 18:42)

Johさん，早々にレスいただき有難うございます．

＞変分じゃなくて微分だったとしたらどうでしょう．

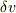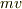えーっと，右辺の $\delta v$ を真中の辺の分母（？）に持ってきて $\delta$ を $\partial$ と考えると，で偏微分するんだから・・，あれっ，確かにになる！そうすると・・，前章で確か，変分と偏微分は入れ替えてもいい事が証明されていましたが，この場合も，替えて同じように考えてもいいという事でしょうか？

Re: 解析力学

ken さんのレス (2005/03/18(Fri) 21:11)

私も数学は苦手なので，いきなり 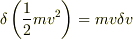$\delta \left(\frac{1}{2}mv^2 \right)=mv \delta v$ と出てくると，ぱっと思い浮かばなかったりします．

私の思考方法はまどろしくって以下のように段階を踏みます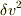． $\delta v^2$ を考えます．

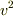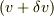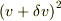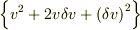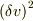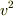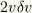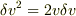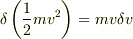えーーと， v^2 の微少な変化を考えるのだから，が $\left( v+\delta v \right)$ になったと考えて， $\left( v+\delta v \right)^2$ を展開すると， $\left\{ v^2+2v\delta v +\left(\delta v\right)^2 \right\}$ になる． $\left(\delta v \right) ^2$ の項は微少の２次だから無視して，もとの値 v^2 を引いて，残った変分は $2v \delta v$ になると． $\delta v^2=2v\delta v$ より $\delta\left(\frac{1}{2}mv^2 \right)=mv \delta v$ ．

ふう．大学時代はこんなこと考えている間に授業の説明はどんどん進んでいってしまい，ついていけなかったなあ．

Re: 解析力学

やかんさんのレス (2005/03/18(Fri) 23:15)

kenさん＞う〜ん，なるほどー！わかったー！(^o^)／やっぱり思い切って質問させていただいて良かったです！ Johさん，kenさん，本当に有難うございました．m(__)m

[home] [掲示板] [ページの先頭]