剛体の運動について

takako さんの書込 (2005/03/11(Fri) 10:51)

こんにちは，takakoです．ＣＯさん，おこめさん昨日の質問の件，ありがとうございました．ＣＯさんのＨＰ拝見しました．天文学を研究なさってるそうで…．私も宇宙に興味を持っているので，いま勉強をしています．先輩，とても憧れています．それで，また分からないところが出てきて，質問したいんですが…．

傾斜角αの斜面上を半径aの円柱(または球)が，転がって運動する場合，この物体に働く力を求めます．斜面上の質量Mの質量中心の運動方程式，質点の固定軸まわりの回転角φの運動方程式は次のようになります．

M(d^2x/dt^2)=Mgsin(α)-F M(d^2y/dt^2)=N-Mgcos(α) I(d^2φ/dt^2)=Fa

Iは慣性モーメント，Nは斜面への抗力を意味します．二つめの式の右辺は斜面への束縛条件から0となり，N=Mgcos(α)となります．ここで，円柱(または球)が滑らずに転がる場合，条件として

x=aφ

という式が立てられるそうです．どうしてこんな式が立てられるのか分かりません．教えてください．この式から，Fを求めています．

おこめです．＞ここで，円柱(または球)が滑らずに転がる場合，条件として

＞x=aφ

＞という式が立てられるそうです．ヒントを言うと角度の定義を調べれば，すぐに分かります．

う〜ん・・・

あっ，分かりましたっ．角度の定義より，弧の長さは，円の半径と角度に比例します．滑った斜面と転がった弧の長さは等しいので

x=aφ

この式は，角度と弧の比例式だったんですね．

おこめさん，またまたありがとうございました．この考えが間違っていたら訂正お願いします．

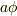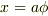もう大丈夫そうですね． $a\phi$ が「回転した弧の長さ」で，が「移動した距離」です．そして円柱(または球)が“滑っていない”というのは，「回転した弧の長さ」と「移動した距離」が等しいという場合ですね．式で書いたら， $x=a\phi$ になります．

これと同じように考えると，「回転した弧の長さ」＞「移動した距離」…回転しすぎ（空回りしている）「回転した弧の長さ」＜「移動した距離」…回転が不足（滑っている）という条件も考えられますね．

> ＣＯさんのＨＰ拝見しました．天文学を研究なさってるそうで…． > 私も宇宙に興味を持っているので，いま勉強をしています． > 先輩，とても憧れています．

研究・・・と，とりあえず「勉強中」と言っておきます． (^^; 宇宙に興味ですか．もし将来的に天文学を勉強してみたいと考えているのでしたら，いくつかアドバイスができると思います．そのときはお気軽にメールください ;)

山本さん，ありがとうございました．全く滑らずに転がる場合と，完全に滑りながら転がる場合だけしか考えていませんでしたが，言われてみると，その中間もあるんですよね．う〜ん…運動の仕方は奥が深いです．

TO ＣＯさん

はい，メールさせて頂きたいと思います．天文学研究室の現場の声を聞けるなんて感激です．