質問です.
質問です.
takako さんの書込 (2005/03/10(Thu) 10:39)
はじめまして.私は転部を目指して物理学を独学で勉強している大学1年生です. 今,力学を勉強しているのですが,分からないところが出てきました. 質問は次の通りです.
位置ベクトルr'=(x,y,z)|r'|=(x2+y2+z2)1/2 ('はベクトルを意味します.付いている数字は全て指数です.)を各成分で偏微分すると,どうして次のようになるのですか.
@r/@x=x/r , (@r/@x,@r/@y,@r/@z)=r'/r(@は偏微分のことです.)
皆さんには,ばかげた問題かもしれませんが,分からないので,もしよかったら教えてください.
Re: 質問です.
CO さんのレス (2005/03/10(Thu) 11:31)
こんにちは takako さん.
偏微分の計算方法についてはOKですね? 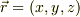 ,
, 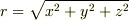 ということを念頭において計算します.
ということを念頭において計算します.
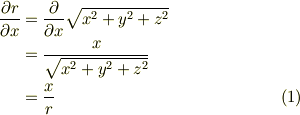
となります.これでわかるでしょうか? 同様にして,y, z についても

となります.
あとはベクトルのほうですね.(1),(2),(3) を用いれば
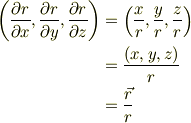
となります.どうでしょうか?
Re: 質問です.
takako さんのレス (2005/03/10(Thu) 13:01)
COさん,丁寧な解説ありがとうございました.今,春休みで教授に質問できなかったので,本当に助かりました. これからも,物理学を勉強していく上で分からない箇所が出てきた時に,助けていただけたら幸いです.
Re: 質問です.
takako さんのレス (2005/03/10(Thu) 13:41)
よく考えてみたら,とても簡単な問題だったんですね.偏微分にまだ慣れていないせいか,分母に(x^2+y^2+z^2)^1/2を付けるのを忘れていました.ご迷惑おかけしました.恥ずかしー….
Re: 質問です.
おこめ さんのレス (2005/03/11(Fri) 01:20)
takakoさん,はじめまして(もういないかな・・・).
>偏微分にまだ慣れていないせいか,分母に(x^2+y^2+z^2)^1/2を付けるのを忘れていました.
「付け忘れ・・・」というのが気になりますね.僕の勘違いかもしれませんが,単なる計算間違えでないような気がします.根本的な解決になるか分かりませんが,こんな公式を覚えておけば間違わないと思いますよ.
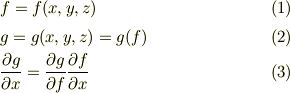
今回の場合は
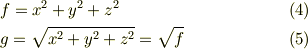
とすれば,計算が簡単になるというわけです.実際に計算を示すと
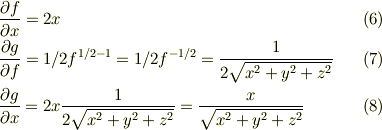
ただしこのとき 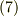 で次の公式の
で次の公式の 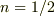 の場合を使っています.(
の場合を使っています.( 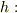 関数)
関数)
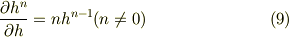
後の 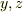 についての偏微分についても同じ方法で求まり,得らるべき結果が,より思考の飛躍無しに出てきます.これで計算間違えも減ると思います.微分及び,偏微分の定義なんかも見直せばもう完璧だと思いますよ.あと,
についての偏微分についても同じ方法で求まり,得らるべき結果が,より思考の飛躍無しに出てきます.これで計算間違えも減ると思います.微分及び,偏微分の定義なんかも見直せばもう完璧だと思いますよ.あと, 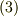 の公式自体の導出なんかも全微分を考えればでる話です.
念のために書いておくと
の公式自体の導出なんかも全微分を考えればでる話です.
念のために書いておくと 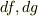 は
は 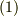 ,
, 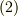 より
より
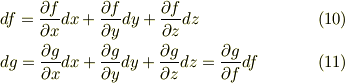
になります. 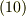 を
を 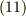 の最後のところに代入することによって
の最後のところに代入することによって
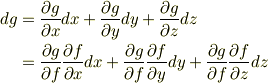
が成り立つことが分かります.両辺を比較すると 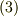 として使った公式が出てくるというわけです.
として使った公式が出てくるというわけです.
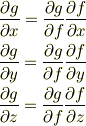
少し説明がくどいような気がしますが,分からなかったところってこんなところだと思うんです(僕個人の意見ですが).この説明が満足いくようなものならば,記事にすることを考えようかな.「掲示板Q&A(偏微分編 Vol.1)」とかいって・・・(書くのはたぶん半年後になりますが)
Re: 質問です.
takako さんのレス (2005/03/11(Fri) 09:55)
おこめさん,ありがとうございました.すごく丁寧な解説で,疑問の余地がありません.全微分から,合成関数の偏微分を求められることを初めて知りました.とても助かりました.
Re: 質問です.
おこめ さんのレス (2005/03/11(Fri) 10:20)
そうですか,それは良かったです.こういう方法は,座標変換などを使って上手に計算を進めようと思えば,よく使うと思います.実際には計算に書かなくても,分かっているかどうかでぜんぜん計算しているときの感覚が違ってくると思います.なので今回の方法はよく憶えておくといいと思いますよ.
Re: 質問です.
CO さんのレス (2005/03/11(Fri) 12:44)
takako さん,おこめさんの丁寧な解説もあり理解が深まったようで良かったですね :) また何か疑問があれば気軽に質問してくださいませ.