力 さんの書込 (2005/02/21(Mon) 17:21)

コリオリの勉強をしていません，スイマセン．今までうろ覚えでいたのですが，皆さんのお話で全く間違った認識をしていた事に気づきました． 二つほど確認させてください． 回転軸と物体の進行方向との角度が大きいほどコリオリの力は強いと説明がありましたが，…垂直落下の場合は赤道付近が一番角度が大きい．ではコリオリ力は垂直落下スル物体には働かないという事でいいのですね？ もう一つ，もし地球が円筒形であったなら，円筒の側面上ではコリオリ力は働かないという事でよろしいでしょうか？

やかん さんのレス (2005/02/21(Mon) 17:46)

力さん，はじめまして．まず，２番目の円筒形の地球，私も想像してたのですが， 大男と赤道列車で考えると，やはりコリオリ力働かないような・・，気がします，がいかがでしょうか？

１番目は，回転軸の方向いてるから，コリオリ力働くような・・，難しいなあ．

やかん さんのレス (2005/02/21(Mon) 20:36)

円筒の地球にはコリオリ力働かず，おぼん型の地球には働く・・・， 本物の地球には，働く・・？？ わかったあ！，運動する物体と，自転軸との距離が変化するときに コリオリ力が働く（と考える必要がある）んだあ！ （円筒は軸との距離かわらないし，おぼんでなくて球でも，北に投げれば 地軸に近づく．赤道に沿って投げれば，やっぱりコリオリ力働かない， ボールを北に投げる赤道地点と真近の着地点をまったいらな平面と近似的に考えるならコリオリ力働かないと近似することもできる！？）

>なんで，そうなの？って聞かれると…回転軸との距離が変化する度合いに応じて，コリオリ力が発生するから…という説明でどうでしょうか．（…あまりわかりやすくないなぁ…）

すいません，山本明さんが，もうお書きになってらっしゃいました・・． きちんと読んでない上に，自分でも思いついたので有頂天になってしまいました． 反省 (^^;

そうすると，垂直落下物体は・・？ 赤道平面で地球をスイカみたいに切ると，お盆型だから，働くような気がするけど 雲や雨みたいにある程度だけ地球にはりついているものと，小惑星みたいに 遠くから来るものでは，違うような・・．だめかなあ・・．

山本明 さんのレス (2005/02/22(Tue) 07:40)

>わかったあ！，運動する物体と，自転軸との距離が変化するときに >コリオリ力が働く（と考える必要がある）んだあ！

大体そういうことでいいと思います．私も最初に行き着いたイメージはやかんさんと同じ．おぼんというか，レコード盤を想像して考えました．自分で思いつくと嬉しいですよね．私も有頂天になりました :)

だけどさらに考えてみると，この考えだけでは不十分な場合もあります． 補足しますと，自転軸との距離が変化しなくても，働くコリオリ力はあるんですね．どういうコリオリ力かというと，地表で眺めて上下方向を変化させるような向きに働くものです．

赤道面から，東に向かってボールを投げるってことを考えてみましょう． そのボールは大体，まっすぐ飛んでいくとすると，次の瞬間地表は少し回転して高さの基準が変わりますね．微々たるものでしょうけど，もともと予測されるよりも高度がちょっと高くなるはずです．地表の人から見ると，真東に向けて投げたボールに，少し上向きの力が働いているように見えると思います． これも速度に比例した効果なので，コリオリ力に分類されるでしょう． （下のひめおかさんへの書き込みに書いた，割り箸の操作をしてみてください．赤道から真東に投げる場合も，２本の割り箸の角度は90度になりますよね）

ただ，こういった地表の人にとっての上下方向のコリオリ力って，あまり考えに入れないんでしょうかね??大抵の議論で「コリオリ力」というと，この上下方向のことは置いておいて，水平面内で働く力を議論している気がします．（私の気のせいかもしれません）

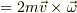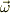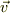ちなみに力さんは，ベクトルの外積なんてものを覚えておられますか？外積記号を使って良いならば，コリオリ力は方向も含めて， (コリオリ力) と表すことができます． ここで観測者の系がどれだけ回転しているかを表す角速度を と書き，運動している物体の質量を ，観測者から見た物体の速度を と書きました． ひめおかさんへの回答では横着したコリオリ力の向きですが「速度方向と回転軸の方向の両方に直交する向き」にコリオリ力が働くわけです．そしてその場合，ひめおかさんが示してくれた 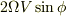という式の は単純に「緯度」じゃなくて，「回転軸と速度の方向のなす角度」になるわけです．少々，複雑になりそうです．

赤道上での巣直落下についても，やかんさんが仰るとおり， >赤道平面で地球をスイカみたいに切ると，お盆型だから，働くような気がする で良いと思います．

外積記号なんて大っ嫌い！というならば，もっと単純に考えることもできます． 赤道上にとても高い塔を立てて，そこから小球を落下させることを考えてみましょう．塔のてっぺんの窓から手を出して小球を落下させると，どこに落下するでしょうか？ Ａ「塔の真横(窓の真下)」，Ｂ「塔の真横から東寄り」，Ｃ「塔の真横から西寄り」，Ｄ「塔の真横から北寄り」，Ｅ「塔の真横から南寄り」，Ｆ「風の向くまま気の向くまま」

・・・まあ，現実的に考えてＡって気はするんですけどね．それともＦか． けど今回は空気抵抗など考えず，理想的な状態で話をしましょう． さらにこの塔はすっごく高い塔だと思っておきましょう． すると，窓から手を出して「小球を離す＝落下させる」と，窓の人から見れば小球が静かに真下に落下を開始しそうだけど，ちょっと離れた位置（地球の外）で考えてみると，小球は「地球の自転につられて東側への速度を持つ」ことになっていることを見いだせるでしょう． そして小球が落下して地表に近づいていくとどうなるか． 塔のてっぺんと比べると，地表付近は回転軸に近づいていますね．つまり，自転の影響で東へ動く度合いが，地表付近では塔のてっぺんよりも弱いということになります．小球は塔のてっぺんと同じだけ東へ動いていく結果，地面よりも多く東へ動くことになるでしょう． 結果として，落下地点はＢ「塔の真横よりも東寄り」が正解になります． これも小球の進行方向に対して横方向に力が働いているように見えて，これも「コリオリ力」です．

同じ現象を地球の外から眺めてみると，なにが起きているのか？っていうと，とての単純な現象です．塔のてっぺんから水平方向に小球を撃ち出したのと同じです．小球は水平方向に初速度を持ち，地球の重力に引かれて，放物線を描いて落下していくでしょう． この現象を，地面と共に動いている人から見ると，先に述べたような理解になるわけです．…コリオリ力が働いて進行方向が少しずつずれていった，と見えるわけです．

まあ，そんな効果が見えるには，よほど高い塔が必要になるんじゃないかって思いますけど…．それに現実問題，空気抵抗とか考えるとこんな単純な話じゃないでしょうね．

>もう一つ，もし地球が円筒形であったなら，円筒の側面上では >コリオリ力は働かないという事でよろしいでしょうか？

大体よいでしょう．けど，あくまで「北へ向かって進む場合に」ですね． 円筒の側面でも，真北に向かっていなかったら，速度に比例して力が（コリオリ力が）働くように見えます．

＜蛇足？：円筒側面，真北に投げて…＞ 円筒の側面で真北に向けて投げたら，コリオリ力は働かないと私は書きましたが，人によっては「それでも地面が回転しているんだから，最初の方で言ってたように，ボールは上の方に動いているように“見える”んじゃない？」と思うかもしれません．その人向けの付け足し． 確かに，真北へ向けて投げたボールも，地球の外から見たら真北じゃなくて少し東側にずれた方向に投げられてます．で，その結果として一瞬後の観測者がいる地点から見れば，少し上昇しているように見えるでしょう． これを「コリオリ力と言わないのか？」というと，「コリオリ力とは言いません」 この現象は「遠心力の効果で，ボールが上昇した」と表現します．

遠心力とは見かけの力のうち，物体が動いていても静止していても働くものを指し，コリオリ力とは“速度の大きさに比例した”ものを指す言葉（…だったはず）です． 正確に見ていくと， 真北へ投げる→遠心力で上下方向にも動き出す→コリオリ力も生じる（遠心力も生じてる） という流れになるでしょう．

やかん さんのレス (2005/02/22(Tue) 11:47)

＞山本明さん ＞大体そういうことでいいと思います． 良かったー！有難うございます．赤道で１ｍ北に投げるのと 北極付近で１ｍ北に投げるのとでは，自転軸に近づく割合が全然違うと 言う事なんですね．塔の話，とってもわかりやすかったです．これも高〜くないと 駄目という事ですね． あと，厳密にはコリオリ力は外積であらわされるから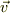， と 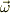の両方に直交する方向に働くという事だったんですね． 力さん，解答いただけたようで良かったですね！

山本明 さんのレス (2005/02/24(Thu) 09:54)

私の回答は無駄に長くて良くないですね． 的確に要約していただき，どうもありがとうございます＞やかんさん．

力さんの理解の助けになれてれば良いのですが…． 回答の不備で，わかりにくいところもあるでしょうから，それについてはどうぞご指摘ください．

やかん さんのレス (2005/02/24(Thu) 13:31)

＞山本明さん ＞私の回答は無駄に長くて良くないですね． とんでもありません．私にも，とってもわかりやすかったので， きっと力さんや，他の読者の方の皆さんにはすごく良く わかったのでは，と思います．

＞的確に要約していただき，

いやー，そんな事ありませんが，でもうれしーです！ :)