ひめおか さんの書込 (2005/02/18(Fri) 15:40)

初めまして．僕は中学二年生です． 今，地球について色々と調べていて，そこで恐らく地学分野に分類されるであろう「コリオリの力」のところで壁にぶち当たっています． そこのコリオリの力の緯度によって働く力の大きさが違う，という部分の，赤道に近付くほど働く力が小さくなり，赤道ではゼロになる，という部分がわかりません． 要するにコリオリの力は慣性の法則が大きく関与していると思うのですが，そう考えれば赤道から極に緯線と垂直方向に運動しても北半球なら右に曲がりますよね？ NHKの高校地学の教育番組映像でも回転する円盤（反時計回り）の縁からボールを転がしたら右に曲がっていきましたし． よく分からないのが，コリオリの力が変わる，というのは具体的にどのような運動をした場合なのでしょうか？ご指南いただけると嬉しいです．宜しくお願いします．

やかん さんのレス (2005/02/18(Fri) 16:02)

ひめおかさん，はじめまして．そうですか，中２ですか． ちゃんと自分の考えも書かれているし，頼もしいですね． 簡単に解説したページがありましたので ご紹介します．ちょっと読んでみてわからなかったら 一緒に考えましょう．最後の方に書いてある，sinとかcosとか， ωとか見慣れない記号は高校でやる三角関数とギリシア文字などですが そこらへんは飛ばして下さい．

• http://www.biwa.ne.jp/~tak-n/phys/coriolis.htm

ひめおか さんのレス (2005/02/18(Fri) 20:02)

迅速且つ丁寧なご説明ありがとうございました． フーコーの振り子についてですよね．これだと確かに地球が自転している，と言うように思います． しかし，フーコーの振り子はそれが存在する緯度によって少しずつずれが生じてくるのではないかと言う幼稚な疑問がひとつ． もうひとつは，この最初の質問についてなのですが，読売新聞東京本社科学記者で気象学者の保坂直紀さんという方が著された「謎解き・海洋と大気の物理」（ブルーバックス社）と言う本の中でコリオリの力について述べられているのですが，そこによると「極でコリオリの力が最大になり，赤道で0に成る，と言うのは例えて言うのであれば極では自転軸に対してフィギュアスケートのようなスピンをしていて，それに対して赤道では自転軸に対して大車輪のような回転をしている．その違いによってコリオリの力の強弱が決まる」とされています．つまるところ，僕の疑問を一言で言えば「赤道から極にボールを投げた場合，そのボールは曲がったように見えるのか？」と言うことを知りたいのです．僕の考えとしては，繰り返しになって申し訳ありませんが，慣性の法則で曲がったように見えるとは思ってるのですが． 「台風は赤道では発生せず，更にこれまでで赤道を通過した台風は存在しない」とされています．しかしそうなると台風は直径はおよそ数百Kmなので，きっとコリオリの力は発生してもいいような気がします．しかし発生しない，と言うのはやはり赤道上ではコリオリの力は0なのでしょうか？ 長くなって申し訳ありません． 疑問として突き詰めると ・コリオリの力は働くとしたらどのような運動をする物体に働くのか？そしてコリオリの力は慣性の法則である程度のレベルまで説明できるのか？ という点です． 幼い質問にご丁寧に答えてくだっさってありがとうございました． もしよろしければ，返信していただけると嬉しいです．

Joh さんのレス (2005/02/18(Fri) 20:44)

コリオリの力は，見かけの力というやつです． 本当に働いている力ではなくて，見ている人が 動いているので，その人から見るとあたかも力 がかかっているように見えるのです．

動いているものは，何か本当の力が働かない限り 慣性だけで動きつづけますので「物は慣性だけで動いている のに，見ている人が変な動きをしているために コリオリの力なんていうものが見えてしまっている」 というのが本当のところです．

おこめ さんのレス (2005/02/18(Fri) 22:09)

ひめおかさんはじめまして．すばらしい文章力ですね．僕も日本語で良いから文章が書けるようになりたいです．

ここからが本題です．ひめおかさんはかなり考え込んでいるようですのでまず見かけの力について書いておきます．

-Jhoさんの仰るとおりコリオリの力は見かけの力です． （見かけの力の簡単な説明） 回転しているコーヒーカップ（遊園地なんかに昔あったやつ）に乗っているヒトが外を見ることを想像してみてください．止まっているはずのモノが動いているように見えるはずです．モノが動いて見えるとき物理ではモノに力が働いていると言います．客観的に見れば止まっているものでも，そのヒトには確かに動いて（力がはたらいているように）見えるのです．

あまり僕は説明能力が無いのでこれくらいの事しか書けませんでした．これ以上の説明が欲しければまた書き込みをしてください．

ひめおか さんのレス (2005/02/19(Sat) 13:27)

johさん，おこめさん，ご丁寧な説明ありがとうございました． 「見かけの力」と言う点は一応理解しているつもりなのですが，コリオリの力による加速度を表す文字式”２ΩＶｓｉｎφ（Ω＝地球の自転角速度，Ｖ＝運動の速さ，φ＝緯度）”について． 勿論中2なのでこんな文字式理解できませんが，緯度を表す「φ」に赤道の緯度である「0」を代入すると僕の知識範囲だとどうしても答えが0に成っていしまうのではないかと思うのです． 本当に何度も繰り返しになって申し訳ありませんが，johさんがおっしゃっていた通り，「全てのものが何か実際の外的な力が加わらない限り慣性で動き続ける．しかしその観測者が自ら動いていかったとしても観測者は自己中心といってはなんですが，地球の自転による自分の移動を自覚できていないので相対的に観測者から見ればきっとその運動している物体に何らかの力が働いた」と感じてしまうだろうと考えているのですが，そうすると上に挙げた文字式に反するのではないか？と言うところがいまの疑問です． 更に細かく言うと，「上の文字式が適応されるのは物体がどのような運動をした場合か」と言うことです． 勿論運動と言っても緯線に平行か垂直か，と言ったように角度の問題だけではなく，その物体がどれだけの距離（緯線にして何度分か）を移動したか，と言うのも視野に入れた方が良い結果が出るのではないかとも思ってはいます． 僕の質問が上手く焦点を絞れたものでなくてすみませんでした． 宜しくお願いします．

ひめおか さんのレス (2005/02/19(Sat) 13:41)

すみません！質問を訂正（追加）させていただきます！ 僕が考えていた質問は「コリオリの力と慣性の法則の境目」でした． 円盤で考えた場合は確かにエンの縁だろうが中心だろうが慣性の法則が問題なく働くので曲がるのは確実です． しかし地球と言う”球体”で考えた場合そうでは有りません．地球の場合極から一定の緯度までは物体はどちらかといえば緯線に対して平行な運動をします．しかし一定の緯度から赤道までは緯線に対して垂直方向の上下運動になります．そうするとそこにはコリオリの力は働かずに，慣性によって（見た目の）運動に影響を及ぼすのではないかと思います． こんなところですいません．用事があるので取り急ぎ追加させていただきます． 返信は月曜日ぐらいになってしまうと思います．すいません． 宜しくお願いします．

Joh さんのレス (2005/02/19(Sat) 15:37)

「上の文字式が適応されるのは物体がどのような運動をした場合か」とのご質問ですが，物体の運動は何でもいいのです．

コリオリの力が働く場合というのは「運動を見る人が，回転運動している場合」です．

やかん さんのレス (2005/02/19(Sat) 16:28)

＞「赤道から極にボールを投げた場合，そのボールは曲がったように見えるのか？」と言うことを知りたいのです．僕の考えとしては，繰り返しになって申し訳ありませんが，慣性の法則で曲がったように見えるとは思ってるのですが． 「台風は赤道では発生せず，更にこれまでで赤道を通過した台風は存在しない」とされています．しかしそうなると台風は直径はおよそ数百Kmなので，きっとコリオリの力は発生してもいいような気がします．しかし発生しない，と言うのはやはり赤道上ではコリオリの力は0なのでしょうか？

私思うのですが，観測者がどこで見てるかということではないでしょうか？ 北極近くでは回転するおぼんの縁にいる状態，一方，赤道付近の人は，北極の人と 比べ，９０度横倒し（おぼんの横にはりついている）で見ていますから，地球の自転によるコリオリ力を考えるのは，やはり極地に近づくほど大きいということでしょうか．台風の回転が左向きなのは北半球のコリオリ力によると言われてますが やはり赤道ではコリオリ力ないだろうし，通過すると回転弱まっちゃうんでしょうかねえ．

FKD さんのレス (2005/02/20(Sun) 21:27)

みなさまはじめまして． FKDと申します．地球物理系の院生をやっています． 物理のかぎしっぽのページはいつも拝見させて頂いています． （とくにVine関係の記事はとても参考にさせて頂きましたです．）

さて，本題です．

＞僕が考えていた質問は「コリオリの力と慣性の法則の境目」でした． コリオリ力というのは慣性力の一種です． 慣性力のうち，回転座標系において物体の進む向きと垂直に 働く力のことをコリオリ力と言います．

＞やはり赤道上ではコリオリの力は0なのでしょうか？ はい．赤道ではコリオリ力は0です．

山本明 さんのレス (2005/02/21(Mon) 11:17)

ひめおかさん，はじめまして． なかなか面白い…というか，とても良い疑問を持たれているように見えます． まず，私がちゃんとひめおかさんの疑問点を理解できているか，確認させてください．ひめおかさんの疑問は，次のようなことで良いでしょうか？

「話を単純にするために，まず地球はデコボコのない球としましょう．さらに空気抵抗を考えるのも止めます．考えるのは，地球の重力だけ．そこに，赤道から極まで…と言わずに，思い切って，投げたボールがノーバウンドで地球を1周してしまうくらい力持ちの男がいたとしましょう． その力持ちの男が，赤道に立って，北極に向かって，真北に，ボールを投げたとき，このボールは北極点を通過するかどうか？」

これを疑問に思っているってので，間違いないでしょうか？ なぜこれに疑問を持っているかは，

「慣性の法則に従うならば，真北に投げてもコースがずれて，北極点には到達しないはず」 だけど， 「赤道に立っているから，コリオリの力は働かない．だから，ボールは真北に向かって飛び続けるのかもしれない」

と，こういう疑問でいいかな？ これだとすると，なかなか面白い疑問だと私は思いました．思わず私も数時間，考えちゃいました． :) 以下，この疑問点への回答をします． もしも，ひめおかさんの疑問が違うことだったら，ごめんなさい．これ以下の文章は，読まなくていいです．

山本明 さんのレス (2005/02/21(Mon) 11:21)

さて，先に答えを言ってしまいますと，この場合，１番目に書いた「真北に投げてもコースがずれて，北極点には到達しない」が正解です．２番目の「コリオリ力が働かない」が間違い．

電車の中から外に向かって，乗客が真横にボールを投げたとしても，ボールは電車の進行方向と同じ方向にも速度を持つことになります．（これを慣性の法則と呼んでいる…のですよね？） それと同じように，赤道で真北に向かって投げたボールは，地球の自転につられて，東(右)へ進む速度の成分を持つことになります．力持ちの男にとって，視界に入っているくらい近い範囲では，自分と同じ速度で東(右)へ進んでいるボールがあたかも狙い通り，真北に向かって飛んでいるかに見えるでしょう． だけど，段々，緯度が上がっていくと，自転で地面が東へ進む度合いは，ボールが東へ進む度合いよりも小さくなってしまいます．地面に立ってる人から見たら，ボールの進行方向が右側へずれていくことになります．そして最終的には，北極点を通ることなく，地球の裏側へ飛んでいきます．

これは，地球の外側から眺めてみると，もっとわかりやすいかもしれません． 赤道から真北へ向かってボールを投げた！…つもりだったのに，実は自転の影響で，北北東くらいの方角に投げていたんですね．あとはボールは勝手に運動しますから，北極点を通過せずに，地球をぐるぐるまわることになります．

さて，それじゃあ，これは「コリオリ力と矛盾する」でしょうか？ 答えは「矛盾しません」． この辺，ひめおかさんが「上の文字式が適応されるのは物体がどのような運動をした場合か」という質問をしていることに関連しそうですね． 確かに“上の式”をよく理解することが大事です． まだ，やや曖昧さを残した説明をしてしまいますが，ご勘弁を．

＞２ΩＶｓｉｎφ

という式ですが，ここのΦは，「観測している人の緯度」ではなくて，「運動している物体の緯度」を代入するべき文字です．そしてΩは，観測者が，どれだけの速さで回転しているか（いまの場合は地球の自転の速さと一致）を表します．Ｖというのは，運動している物体の速さ． （“曖昧さを残した”と言ったのは，力が働く向きについて，正確な言い方をしていないからです．…これはちょっと面倒なので，許して）

さて，Φが観測者の緯度じゃないとわかれば，結果は想像できるでしょうか． 赤道で投げたボールも，緯度が段々上がっていけば，コリオリ力を受けることになり，進路が右に逸れていきますね．上で説明した状況と，まったく同じです．

要するに，

>コリオリの力と慣性の法則の境目

コリオリの力と慣性の法則の境目はありません． 慣性の法則に従って地上の人の狙いから進行方向がずれていく効果が，地上の人から見るとコリオリ力で進行方向がずれたように見えるよってこと．同じ現象を，別の言葉で説明しているだけです．（慣性の法則の方が，もっと適用範囲は広いですけど）

山本明 さんのレス (2005/02/21(Mon) 11:23)

赤道でコリオリ力が働かないことについては，

> 地球の場合極から一定の緯度までは物体はどちらかといえば緯線に対して
> 平行な運動をします．しかし一定の緯度から赤道までは緯線に対して垂直
> 方向の上下運動になります．そうするとそこにはコリオリの力は働かずに，

の説明がなかなか良さそうに見えます．ただ「緯線」と書いてあるところが，私にはやや曖昧に見えますので，次の説明をお勧めします．

「回転軸(この場合地球の自転軸)と，物体の進行方向の間のなす角度が大きいほど，コリオリ力は強く働く」

ということ． 割り箸でも用意してみましょう．１本は，地球の回転軸の方向に合わせておきます．もう1本は，物体の進行方向に向けてみましょう． 赤道上で物体を真北に投げるときは，物体の進行方向と回転軸，同じですね．割り箸のなす角度は0度．だからコリオリ力も0． 緯度が上がっていくと，だんだん，2本の割り箸のなす角度が大きくなるでしょう．そして北極間近になると，2本の割り箸のなす角度は90度で，一番大きくなります．コリオリ力も，一番大きくなります．

なんで，そうなの？って聞かれると…回転軸との距離が変化する度合いに応じて，コリオリ力が発生するから…という説明でどうでしょうか．（…あまりわかりやすくないなぁ…）

さて，ここまで連続して投稿した内容，ひめおかさんが中２ということを知った上で，全く遠慮せずに，かなり難しい話をしました．全部わからなくておかしくないし，もしどこか特にわからなくて，もっと知りたいって部分があったら，遠慮なく言ってください．改めて，説明しなおします． …返答には時間かかるかもしれませんけど． それでは，長々と失礼しました．

ひめおか さんのレス (2005/02/21(Mon) 13:54)

johさん，やかんさん，FKDさん，山本明さん，わかりやすい回答ありがとうございました． 山本さんのおっしゃっていた「ノーバウンドで地球を一周」という発想は，僕にはありませんでした．確かに，そのくらいのスケールで考えたほうが格段に解り易いことに気づきました． 山本さんのご説明の内容は，言い換えれば「コリオリの力が働かないのは赤道であるけれど，それは赤道《一点》を見た場合である」と言うことでいいのでしょうか？ よく考えてみればそれはFKDさんがおっしゃっていたことに繋がりますね． このようなことに気づかずに皆様にご迷惑をかけてしまって申し訳ありませんでした． 本当にありがとうございました．やっと合点がいきました．

山本明 さんのレス (2005/02/21(Mon) 16:39)

>「コリオリの力が働かないのは赤道であるけれど，それは赤道 >《一点》を見た場合である」と言うことでいいのでしょうか？

バッチリ，ＯＫです．

ただ赤道一点だけでなくても，十分近い場所ならば，コリオリ力はかなり小さくなるでしょう．ある一定の緯度までは，ほとんどコリオリ力の効果を無視してしまっていいくらいに．

例えば，赤道から500km離れた位置だと…雑な計算ですが，それは緯度にして4〜5度くらい．(確か地球の半径は6500kmくらいだったから，一工夫すれば計算できますね)．そのときのsinΦはおよそ 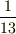です． Ωは地球の自転を考えれば1日に360度回転するとして，およそ 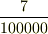[rad/s]という数字になります（角度の単位にradという高校範囲の知識を使っています）． Ｖとしては…台風の風速として 15 [m/s]なんかを考えてみましょうか． するとコリオリ力によって生じる加速度は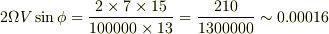， [m/s^2]． ちなみに重力による加速度は大雑把に 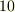[m/s^2]なので，コリオリ力の効果は重力に比べてかなり小さいですね．…重力の効果のせいぜい 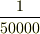かな． …実はＶにどんな値を代入するのがもっともらしい考察なのか，私はよく知らないので，かなり適当なことを言ってるかもしれません．…きっと，極端にヤバい計算をしていたら，FKDさんが指摘してくれるはずっ!!と期待してます (^^; (どうぞ，よろしくお願いします＞FKDさん)

とにかくまあ，赤道からちょっと離れたくらいでは，コリオリ力はほとんど0になりますよ…って話です． 赤道からどれくらいの距離から，台風は発生できるんでしょうね． …その辺の話は，私よりもひめおかさんの方が詳しそうです :) どうぞ，この調子でいろんなことに興味を持って，考えて，考えて，調べたりしていってください．

蛇足： “ノーバウンドで地球を１周できる”速さのことを，「第一宇宙速度」と呼んでいます． で，地球上でそんな速さでものを投げられる人はいないでしょうけど，もっと軽い星だったらどうかなぁ…って話が，この物理のかぎしっぽ「力学＞色々な運動＞手投げ人工衛星」ってページで，考えられています．難しい計算の話もあるけれど，雰囲気を楽しんでもらえたら嬉しいです． ご参考までに． → http://www12.plala.or.jp/ksp/mechanics/handSatellite/index.html

やかん さんのレス (2005/02/21(Mon) 17:35)

Johさん，おこめさん，ＦＫＤさん，山本明さん，こんにちは！ ひめおかさん，いっぱいレスがあって良かったですね． 特に山本明さんの力作は私にとっても勉強になりました．

私の書いた， ＞私思うのですが，観測者がどこで見てるかということではないでしょうか？ 北極近くでは回転するおぼんの縁にいる状態，一方，赤道付近の人は，北極の人と 比べ，９０度横倒し（おぼんの横にはりついている）で見ていますから，地球の自転によるコリオリ力を考えるのは，やはり極地に近づくほど大きいということでしょうか．台風の回転が左向きなのは北半球のコリオリ力によると言われてますが やはり赤道ではコリオリ力ないだろうし，通過すると回転弱まっちゃうんでしょうかね

は，大変怪しげなので忘れてくださいね（なんか間違ってるぽいです）．

山本明さんの，うまい例え話（力持ち男と電車）と，地球の自転止める話（不思議がいっぱいさん，アイデアお借りしました：すいません他のスレです）で思いついたのですが（完全なパクリですが），いっその事，地球の自転止めて，赤道上に線路を一周しいて，力持ち男に乗車してもらい，北側の車窓から，ボールを投げてもらった，と考えても同じ事でしょうかね．投げ終わってからも力持ち男は常に真北を向いている車窓から見ると（もちろん車窓の視野の左ですが），確かに投げたボールは東にずれている，とか．同じ事ですね（パクってすみません・・）．