不思議がいっぱい さんの書込 (2005/02/18(Fri) 09:59)

はじめまして．物理素人の素朴な質問です． 振り子運動と円運動は，なぜ横から見ると同じ全く同じ運動のように見えるのですか？（つまり，横から見るとどちらも振り子運動のように見える） 素人の私でもわかるよう，よろしくお願いします．

EM さんのレス (2005/02/18(Fri) 14:49)

簡単のために等速円運動についてのみ考えます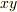． 平面内で質点が等速円運動をしているとして， 質点の位置を極座標 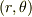で表すと，

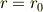
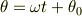
ここで 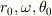は定数です． これを 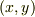座標で表示してやると，

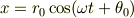
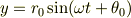
となり，それぞれの式が単振動を表す式になります． 要するに今の場合の等速円運動は 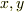方向の単振動の重ね合わせで成されているということになります． この運動を横から眺めてみるのですが，自分の眺めた方向を 方向と考えると 方向の運動だけを見ていることになるので 方向についての振り子運動だけが見えることになります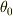．( を適当にとってやることで，そういうふうに軸をとることは可能です．)

やかん さんのレス (2005/02/18(Fri) 18:06)

不思議がいっぱいさん，ＥＭさん，こんにちは．

＞振り子運動と円運動は，なぜ横から見ると同じ全く同じ運動のように見えるのですか？

不思議がいっぱいさんの学年がわからないので（小学生か，中学生か，高校生か，専門外の大学生か）難しいのですが，振り子も円運動も横（上？）から影にして見たとき，（１）振り子での中心からずれた距離と，そこでかかる力による加速度との関係と，（２）等速円運動における中心からずれた距離とそこでかかる加速度との関係が同じ決まり方をしている（比例している）から，同じ運動のように見える，という事でどうでしょうか．

Joh さんのレス (2005/02/18(Fri) 18:48)

横から見たとき，実は同じではありません． 公開されたばかりの「楕円積分〜振り子の周期を求める」をご覧下さい． (自分の書いた記事の広告...^^)

簡単にいいますと，円運動も振り子の運動も周期的な運動です． これは，見ていたら周期的なんだなぁと誰でもわかるはずです． (コロコロ転がっているものと，揺れている振り子を想像ください． 何度も同じ状態に戻ってきます．)

何に関して周期的なのかというと，角度ですね．そこで，円運動も 振り子の運動も，角度の周期関数で表現できるはずだ！と考えます． このあたりから，物理っぽくなってきましたが，思考の流れとしては ごく自然だと思います．

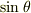結論から言うと，等速円運動というのは，この角度の関数という部分が一番簡単な になっていますが，振り子の運動では になっているのです．ただし，この角度が非常に小さいと近似すると，

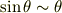
と考えても，まぁいいでしょう．そうすると，式の上では等速円運動と同じになるということだったです．

一般的に，周期的な運動(例えば１２０００年毎に氷河期が来るとか，そんなスケールの大きい周期運動でも良いです．)は，何か周期関数で表現できるはずです．フーリエ変換という技と使いますと，大抵の関数は三角関数で表現できてしまいます．そして，そんな色々な周期運動も，一番大胆で乱暴な近似を行ってしまうと，円運動と同じようになってしまうのです．

どんな周期現象でも(横から見ると！？)円運動と同じに見えるかと言えば，部分的には似たように見えると言えるでしょう．ただし，これが一番荒っぽくて単純化された近似だということを忘れないで下さい．身の回りで，周期的なものを探してみると，面白いと思います．

やかん さんのレス (2005/02/18(Fri) 19:15)

Johさん，こんにちは． >横から見たとき，実は同じではありません． 振り子の運動では〜と考えても，まぁいいでしょう．そうすると，式の上では等速円運動と同じになるということだったです

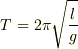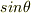なるほど．そうすると，振り子の も と の 近似から得られるのですね．勉強になりました．

不思議がいっぱい さんのレス (2005/02/19(Sat) 06:47)

EMさん，やかんさん，Johさん，ご回答ありがとうございました．素人の私には難しすぎてよくわからなかったんですが，つまり，両運動は同じように見えるだけ，見掛けだけ似ている運動にすぎない，ということで理解していいのですか？

やかん さんのレス (2005/02/19(Sat) 12:05)

う〜ん，いいと思います．近似できるという事だから，振り子のふれが小さいときは計算上も同じと扱って差し支えない，という事でしょうかね（全く同じだ！と断定すればもちろん間違いを言ってることになるし，ほぼそっくりに数式で扱える状況なのに，必要以上に”本当はこの式いい加減なんだ！”と見下して扱う必要もないでしょうね．ある条件下で，ある精度で実用上使えればいいわけですから）．物理は数学ではないので結構近似で話を通してるところありますよね．特に高校から習う古典的な物理は多いのかな．

不思議がいっぱい さんのレス (2005/02/20(Sun) 02:40)

やかんさん，お返事ありがとうございます．すみません，もう少し質問です． 振り子運動も加速度運動も重力の問題ですよね？えーっと，つまり等加速度が物体を動かすエネルギーで，重力がそれを邪魔してる，という風に解釈してるんですが，あってますか？もしそうなら，円運動は重力と関係あるのかな，もしかして同じ運動なのかな，とふと思ったんです．天体は円運動してるうえ，重力を持っているから．．．円運動してなくて重力を持つ天体もあるんでしょうか？

崎間 さんのレス (2005/02/20(Sun) 07:10)

> 振り子運動も加速度運動も重力の問題ですよね？

振り子はそうとも言えるかもしれませんが，「加速度運動」では言葉の意味する範囲が広すぎますので，重力の問題とは限りません．

> えーっと，つまり等加速度が物体を動かすエネルギーで，
> 重力がそれを邪魔してる，という風に解釈してるんですが，あってますか？

振り子の場合は，重力が運動の源になっています．おもりが重力によって下に引かれるから，揺れています．エネルギーは，最初に「振り子を持ち上げたとき」に与えた，ということになります．加速度というものは，エネルギーでも力でもありません（これらに関係はします）．

> 円運動は重力と関係あるのかな，もしかして同じ運動なのかな，

これは，鋭い洞察かもしれません．円運動は，向心力と呼ばれるものによる運動です．遠心力という言葉は普通に使いますよね？ 車が急カーブするときなどに，外側に引かれる力です．中心力とはその逆で，円の中心に向かって引かれる力です．天体，たとえば地球の円運動は，太陽の重力に引かれているからです（正確には円ではなく，太陽を一つの焦点とする楕円軌道を描いています）．振り子の場合は，おもりをぶら下げている糸（かなにか）の張力が向心力となります．

> 円運動してなくて重力を持つ天体もあるんでしょうか？

円運動していない天体ですか．なにかしら重力の影響を受けいていると思いますので，天体はなにかしら運動していると思いますが詳しいことは存じておりません…．正確に円運動している天体は，あまりないのではと．質量は，どの天体ももっていると思います．

ken さんのレス (2005/02/20(Sun) 16:20)

> 円運動してなくて重力を持つ天体もあるんでしょうか？

太陽はまったく円運動をしていないと思っているのですが， いかがでしょうか？

不思議がいっぱい さんのレス (2005/02/21(Mon) 01:51)

kenさん，でも太陽は太陽系内では静止して見えますが，銀河系内で見ると渦巻き運動してますよね．渦巻き運動は円運動とも楕円運動とも関係ないのかもしれませんが．．．

＞正確に円運動している天体は，あまりないのではと．

おっしゃる通りですね．私が「円運動」と言い切ったので誤解を招いてしまいました．舌足らずですみません．円運動でも楕円運動でも，観察者側に一番近い位置からむこうへ曲がっていき観察者側に一番遠い位置に行くまでの横から見た動きが振り子の両端の動き(スピードを落とし静止し逆方向にスピードを増す）に似て見えるのがすごく不思議だったんです．

＞振り子の場合は，重力が運動の源になっています．おもりが重力によって下に引かれるから，揺れています．エネルギーは，最初に「振り子を持ち上げたとき」に与えた，ということになります．加速度というものは，エネルギーでも力でもありません（これらに関係はします）．

誤解を正していただいてありがとうございました．よく考えてみると小学校の時に勉強しましたよね！(恥）

遠心力と中心力についてですが，地球でいえば公転運動が中心力を生み自転運動が遠心力を生むんですよね？それとともに重力が働いていることで，地球上のものが遠心力によって宇宙空間に散らばっていったり，中心力によって地中に埋もれていったりしないんですよね？すると，３つのこれらの力が今の状態を保っているわけですよね？じゃ，もし何らかの理由で地球の自転がとまったらどんなことが起こるのでしょう？（ありえないかな？）

やかん さんのレス (2005/02/21(Mon) 13:40)

ＥＭさん，Johさん，崎間さん，kenさん，こんにちは！いつもお世話になります．

＞遠心力と中心力についてですが，地球でいえば公転運動が中心力を生み

太陽を中心とする地球の公転運動が遠心力を生み，それが太陽からの重力と釣り合ってるんで，地球の軌道がかわらないんでしょうね．

＞自転運動が遠心力を生むんですよね？それとともに重力が働いていることで，地球上のものが遠心力によって宇宙空間に散らばっていったり，中心力によって地中に埋もれていったりしないんですよね？

地球を基準に考えればそうなんでしょうね．重力弱ければ星になってないんでしょうね．

＞すると，３つのこれらの力が今の状態を保っているわけですよね？

えーっと，（１）太陽から地球に働く重力と地球の公転による遠心力，（２）地球の自転による遠心力と地球の重力，それぞれが釣り合ってるんでしょうかね．

＞じゃ，もし何らかの理由で地球の自転がとまったらどんなことが起こるのでしょう？（ありえないかな？

おお，ＳＦ映画みたいですね．確か映画のストーリーか何かでは，大気には自転の慣性があって急に止まらないから，自転の速度と同じ突風が吹く，だったかな？（ＨＧウエルズか誰かの小説にあったような・・．記憶違いかな）ご質問とは違いますが，よく核戦争で地球の自転軸がわずかでもずれると，人類が生存できないぐらい，大嵐とか，異常気象がおきるとか言いますけどねえ・・．ホントかな？

不思議がいっぱい さんのレス (2005/02/22(Tue) 08:59)

やかんさん，いろんな問題に取り組んでいらっしゃるようで大変ですね（笑）．私の素朴な疑問に取り組んでいただいてありがとうございました．私達地球の住人達は公転＆自転＆地球の重力だけでなく，太陽や月や他の惑星達の重力もからむ複雑なバランスの上に成り立っているんでしたね．

＞地球の自転軸がわずかでもずれると，人類が生存できないぐらい，大嵐とか，異常気象がおきるとか言いますけどねえ・・．ホントかな？

核戦争とか小惑星激突でこのバランスがあっという間になくなったりするわけですね．宇宙って不思議だな．その不思議を計算できたり理解したりする物理屋さんは素晴らしいな，と思います．また，不思議がわいてきたらおじゃましますね．みなさん，ありがとうございました．

やかん さんのレス (2005/02/22(Tue) 11:08)

>やかんさん，いろんな問題に取り組んでいらっしゃるようで大変ですね（笑）．

いやあ，取り組むなんてちゃんとしたものじゃなくて，私の場合，面白いのでパッと書き込んじゃうから，間違いも多い（の方が多い）と思います．私もっと良く考えてからでないと駄目ですね (^^;

＞核戦争とか小惑星激突でこのバランスがあっという間になくなったりするわけですね．

ホント，はかないですねー，人類は．天文も含め，物理は素人ですが，何年か，何十年か前に，小惑星かなんだかが木星にぶつかったとか．木星だから良かったけど，地球だったらたまりませんよねえ．w(☆o◎)w

＞その不思議を計算できたり理解したりする物理屋さんは素晴らしいな，と思います．

全くそうですよねー．私も本当に憧れましたが，こちらに来させて頂いていると，やはりきっと，私ではついて行けなかっただろうなあ，と思います．憧れは憧れのままがいいのかも・・． また是非いらしてくださいねー(＾-＾)/

ken さんのレス (2005/02/22(Tue) 21:10)

不思議がいっぱい さん，やかんさんこんばんは

>銀河系内で見ると渦巻き運動してますよね

あれって，銀河系の星が渦巻状に分布しているのであって， 渦を巻くように回転運動しているとは思っていませんでした． 銀河系の中心て，どうなっているのだろう？

＞確か映画のストーリーか何かでは，大気には自転の慣性があって急に止まらないか ＞ら，自転の速度と同じ突風が吹く，だったかな？

想像ですが， 自転が急激に停止した場合→「大気は急に止まらないから自転の速度と同じ突風 が吹く」のは，正しいでしょうが，地上にある全てのものが急に止まらないので，家屋や樹木や人間も吹っ飛ばされます． 自転がきわめて緩やかに停止した場合→大気も緩やかに停止しますが，そのうちずっと太陽の方を向いて灼熱になる部分と，ずっと日があたらず極寒の部分との間で対流がおき暴風が吹き荒れます．

＞何年か，何十年か前に，小惑星かなんだかが木星にぶつかったとか．木星だから良かったけど，地球だったらたまりませんよねえ．

数十億年というスケールで見た場合，地球には何回か巨大隕石が落下し，そのことによって人類が進化したともいえます．地球の黎明期に小惑星がいくつかぶつかってきたおかげで，地球が現在の大きさになり，衝突の膨大なエネルギーによる熱が現在も地球の中心部を6000℃の高温のどろどろの状態に保っています．このことが火山や地震，大陸の移動を生みそれが生命の進化につながったいうことを，去年のＮＨＫ「地球大進化」で知りました．

やかん さんのレス (2005/02/23(Wed) 00:42)

kenさん，こんばんは！

＞あれって，銀河系の星が渦巻状に分布しているのであって， 渦を巻くように回転運動しているとは思っていませんでした． 銀河系の中心て，どうなっているのだろう？

あっ，そういえば，以前TVの科学番組でやってたのですが，確か kenさんのおっしゃるように，銀河は渦巻状に分布してるだけで ねじれるように回転してるんじゃなくて，全体が，ぞろっと 回転してるような事言ってました．みてくれのイメージとちょっと違うんでしょうかね． 銀河系の中心は，いて座の方向で，ブラックホールあるとかいうけど 本当なのかなあ？

＞自転が急激に停止した場合→「大気は急に止まらないから自転の速度と同じ突風 が吹く」のは，正しいでしょうが，地上にある全てのものが急に止まらないので，家屋や樹木や人間も吹っ飛ばされます． 自転がきわめて緩やかに停止した場合→大気も緩やかに停止しますが，そのうちずっと太陽の方を向いて灼熱になる部分と，ずっと日があたらず極寒の部分との間で対流がおき暴風が吹き荒れます．

おお，いずれも物騒ですねえ．でもきっと，こういう一大事には，ゆっくりでなくて，キュッと止まって，前者のような悲惨な事になっちゃうんでしょうか？ (^^;

>数十億年というスケールで見た場合，地球には何回か巨大隕石が落下し，そのことによって人類が進化したともいえます．地球の黎明期に小惑星がいくつかぶつかってきたおかげで，地球が現在の大きさになり，衝突の膨大なエネルギーによる熱が現在も地球の中心部を6000℃の高温のどろどろの状態に保っています．このことが火山や地震，大陸の移動を生みそれが生命の進化につながったいうことを，去年のＮＨＫ「地球大進化」で知りました．

地球に磁極があって，太陽風などから守られているのも，自転とドロドロのおかげでしょうから，そうすると，生まれるも宿命，滅びるも宿命という事なんでしょうかねえ・・（感慨）． :)