問題を考えてみたのですが，ちゃんとした回答ができません．

nadja さんの書込 (2005/02/16(Wed) 11:44)

＜問題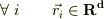＞ $\forall\ i\qquad \vec{r_i}\in{\bf R^d}$ のd次元平坦なEuqlid空間において，任意のi,jで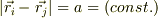， $|\vec{r_i}-\vec{r_j}|=a=(const.)$ となる点の集合Iの濃度 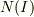N(I) はd+1以下である．

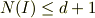
$N(I)\leq d+1$

たとえばd=2の場合は三角形，d=3の場合は正四面体である．

あ，ちなみにaには大して意味があるわけではなく，等間隔な点集合の濃度の上限を問題にしています．直感的には解けるのですが，どのようにとけばいいのでしょうか？

追記ですが，これは自分で考えた統計力学とかで出てくる無限レンジモデル（比較的解析解が出しやすい）の，空間（phase space）でどのように結合しているかなぁと思って作りました．

僕の研究対象のスピングラス（物性）の中の「超計量空間」とか「カスケード構造」とかに関係しています．