質問です.
質問です.
nadja さんの書込 (2005/02/16(Wed) 08:20)
どうしても解けそうで解けない積分があります.正規分布に従う確率変数Xの1/Xの期待値
![E[\frac{1}{X}]=\int_{-\infty}^\infty\frac{dx}{\sqrt{2\pi\sigma^2}}\frac{1}{x}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)](http://hooktail.maxwell.jp/bbslog/411cb820b9a36c5bd0c61d503c00c50c.png)
です.どのようにとけばいいのかわかりません.教えてください.
Re: 質問です.
CO さんのレス (2005/02/16(Wed) 08:58)
こんにちは, nadja さん.
どうも収束しないような気がするんですが,この問題の出所を教えていただけますか.
また  は
は 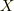 の関数のようですが,右辺には
の関数のようですが,右辺には 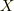 が現れてきていませんね.
が現れてきていませんね.
Re: 質問です.
ken さんのレス (2005/02/16(Wed) 10:25)
kenです.
こんにちは, nadja さんCOさん.
正規分布の確立密度関数自体解析的に計算できないです. だから,正規分布表なるものが使われています.
正規分布の確率関数関数 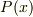 は
(nadja さんの質問に書かれていますが改めて書きますと)
は
(nadja さんの質問に書かれていますが改めて書きますと)
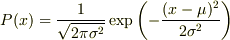 ですよね.
ですよね.
nadja さんは,質問文で正確にかかれていることから,わざわざ述べることもないですが,大学2年生以下にもわかるように,かつ自分の確認のために以下書きますと.
ここで,P(x)はX=xのときの確立の密度ですよね.
そこでf(x)=1/xの関数の期待値Eを計算するためには
f(x)P(x)をxの取りうる範囲の全てにわたって積分してやればいいという
ことですよね.xが 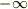 から
から 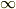 までとりうるので
までとりうるので
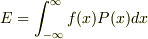 を計算してやればいいと.でも,これをそのまま解析的に解くのはできなさそうです.
を計算してやればいいと.でも,これをそのまま解析的に解くのはできなさそうです.
ところで 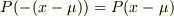 ですよね.
さらに
ですよね.
さらに 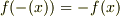 .
.
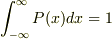
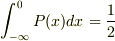
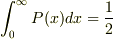 ああ,
ああ, 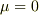 なら
なら
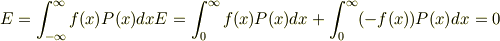
と簡単に0と求まるのだけど...
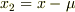
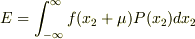
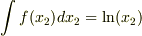 のもとでうまく求められるだろうか.
f(x)=1/xがx=0で無限大に発散するため求められないような...
いやx→+0でプラスの無限大に,x→-0でマイナスの無限大に
発散しP(x)はx→+0でもx→-0でも同じ値なのでうまく打ち消しあって
ある値になるかもしれない.
のもとでうまく求められるだろうか.
f(x)=1/xがx=0で無限大に発散するため求められないような...
いやx→+0でプラスの無限大に,x→-0でマイナスの無限大に
発散しP(x)はx→+0でもx→-0でも同じ値なのでうまく打ち消しあって
ある値になるかもしれない.
Re: 質問です.
nadja さんのレス (2005/02/16(Wed) 10:55)
僕の論法はこうです.
次の特性関数 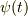 を定義します.
を定義します.
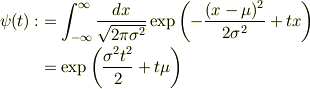
これを使うとある自然数n乗の期待値は
![E[X^n]&=\frac{\partial^n}{\partial t^n}\psi(t=0)\\&=\frac{\partial^n}{\partial t^n}\int_{-\infty}^\infty\frac{dx}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}+tx\right)\qquad (t=0)\\&=\int_{-\infty}^\infty\frac{dx}{\sqrt{2\pi\sigma^2}}x^n\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)](http://hooktail.maxwell.jp/bbslog/275f79c12ac8fb7735ab48f0cd7c3797.png)
となる.これは統計の母関数,統計力学の分配関数に相当する物を使って計算しようと思ったのですが,この方法を使おうとすると,-1乗の偏微分という未定義にぶつかります.
どうしたらいいのでしょうか?
Re: 質問です.
nadja さんのレス (2005/03/27(Sun) 05:00)
以前研究室の人に聞いたのですが,この正規分布の性質がよいからといってすべての関数の期待値を定義できるとは言い切れないそうです.
なのでためしに数値計算でどのように動くか計算してみようと思います.
お騒がせしました.
では,