無題

ファインメンさんの書込 (2005/02/12(Sat) 18:10)

ついこの間，下のボッシュさんのスレッドで初めて書き込みをさせてもらったファインメンと言います．物理学科のものです．質問させていただきたいので，よろしくお願いします．

統計力学での基礎の基礎「等確率（等重率）の原理」というものがありますよね．今まではあまり疑問に思わずに，その考えを受け入れて熱・統計力学の勉強を進めてきたのですが，不明な点にあたってしまい，どんどん定義に還っていったところ，突然壁に当たりました．その定義が岩波書店出版の「統計力学」によると「孤立したマクロな物体では，十分に長い時間で見ると，実現可能な量子状態はすべて等しい確率で実現する．」とあります．ここで，例えば，ある閉じ込められていて孤立した空間の中にN個の原子があり，そのいくつかは電子が励起状態にある原子があるとして，その状態が初期状態だとします．すると，基本的にエネルギーの低いほうに状態は向かうと思うのですが，等重率の原理からすると，ある一つの原子が，他の励起状態にある原子のエネルギーを全部受け止めて，とても高いエネルギー準位にあることが初期状態と同じ確率で起こりうるというふうに受け取れます．でも，一般的にこの二つは同じ確率では起こりえないと思うのですが・・・この考え方のどこがまずいか，教えていただけないでしょうか？よろしくお願いします．

Re: 無題

CO さんのレス (2005/02/12(Sat) 18:38)

> 等重率の原理からすると，ある一つの原子が，他の励起状態にある原子のエネルギーを全部受け止めて，とても高いエネルギー準位にあることが初期状態と同じ確率で起こりうるというふうに受け取れます．

実現可能な量子状態を全部書き出してみるとスッキリすると思うんですが・・． 3つの区別ができる原子があって，3つのエネルギー量子を分配する場合を考えると， (3,0,0), (0,3,0), (0,0,3), (2,1,0), (0,2,1), (1,0,2), (1,2,0), (0,1,2), (1,1,1) となります．それぞれの 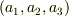(a_1,a_2,a_3) が現れる確率が等しい，というのが等重率の原理です．

Re: 無題

おこめさんのレス (2005/02/12(Sat) 18:53)

付け加えると実際には区別不可能な粒子（COさんの説明では原子）に番号をつけると等重率になる．そういうことだと思います．マクロな対象となるとN〜6.02×１０＾{23}のオーダーになるので全ての粒子がある同じ状態を取るという状態の確率を考えるとすごい低い確率になります．それはその状態の組み合わせの数（この言葉であってるのかな？要するに111は１通り，123は3!=6通り）が１だからです．

Re: 無題

ファインメンさんのレス (2005/02/12(Sat) 19:06)

COさん，おこめさん，返信ありがとうございます．

COさん＞＞確かにその分配については理解できるのですが，例えば(1,1,1)と(3,0,0）は，同じ確率で起きるいうのが直感的に理解できないのです．もちろん，「原理だから．」といわれてしまえばそれまでなのですが・・・(1,1,1)と(3,0,0)では，後者は一つの粒子が高エネルギーであるというこが，すでに不安定なのではと思ってしまいます．「十分長い時間」という条件は，「どちらも起こるけど瞬間を見れば，どちらも起こりうるよ．」といったようなことなのでしょうか？それだとしても，安定している状態のほうが，起こる確率が高いような・・・．何か，根本的に考え方が間違ってるような気がしないでもないのですが，どこが間違っているのかがわかりません．

Re: 無題

CO さんのレス (2005/02/12(Sat) 19:23)

ある状態が安定だとか不安定だとかが，どこから導かれる概念なのかを考えてみると良いのではないでしょうか． :)

Re: 無題

おこめさんのレス (2005/02/12(Sat) 21:18)

僕の書いた補足が反映されてないような・・・

Re: 無題

ファインメンさんのレス (2005/02/12(Sat) 21:31)

COさん＞＞わかりました．その部分から考え直してみます．

おこめさん＞＞コメントすら残さずに，ごめんなさい．もちろん，おこめさんのおっしゃることもわかります．でも，僕が考えているのはその状態数１というのが他の状態のものと同じものか，つまりは等確率なものなのかを考えているのです．なんだか混乱しているみたいなのでお二人の意見を参考にさせてもらいつつ，もう一度自分で考え直したいと思います．ありがとうございます．（＾＾）

Re: 無題

ファインメンさんのレス (2005/02/12(Sat) 21:32)

おこめさん＞＞すみません．上の「他の状態のものと同じものか」→「他の状態のものと同じ重みなのか」という意味でした．

Re: 無題

CO さんのレス (2005/02/12(Sat) 21:59)

ファインメンさん > わかりました．その部分から考え直してみます．

考えがまとまりましたら，また書き込んでいただけると嬉しいです :)

Re: 無題

ファインメンさんのレス (2005/02/14(Mon) 17:00)

COさん，おこめさん＞＞疑問が解決しました．大学での学生実験で，発光スペクトルに関しての実験で，気体分子のエネルギーについて回転エネルギーと振動エネルギーの話がでてきたのを思い出して，それで少々混乱したようです．考えている系がかなり単純であるのを考えれば，等確率の原理は何も（？）不思議でない，というか認めても物理的に差し支えないのもわかりました．ありがとうございました．これからも，大したことのない質問でお世話になるかもしれませんが，よろしくお願いします．

Re: 無題

おこめさんのレス (2005/02/15(Tue) 18:40)

それは良かったですね．関係ないですが，僕も発光スペクトルの実験とかやってみたかったです．僕の大学の実験器具はほとんど壊れているし，そのような感じのカッコいい実験をしたことが無いです．

Re: 無題

peppermint さんのレス (2005/02/15(Tue) 21:23)

はじめまして．最近研究者としての道を貫くかどうか迷っているpeppermintと言います．（といってもまだ学部３回生ですけど）なんかもう疑問が解決してしまっているみたいでなんなんですけど，等重率の原理は「原理」なので，そうすると実験結果と合うんだからしょうがないだろーと言われてしまえばそれまでです．が，一応物理としては原理と言えども納得する説明が欲しいものです．それはエルゴード性の定理（実はまだ厳密な証明は成されていないと聞いています）というモノなのですが，これに依ると

ある観測値の長時間平均＝ある観測値の位相平均（取りうる状態一つ一つの観測値の平均）

が成り立ちます．我々が得る観測値はあるマクロな測定によって，熱平衡状態では長時間平均と一致するでしょう．すると，この等式が成り立つとすると，考えている系は「その"長時間"の間に取りうる全ての状態を同じ確率で実現しなくてはならない」という結論に至ります．そうしなければ位相平均と一般に一致しなくなるからです．

とまぁ，ここまでくると等重率の原理ももっともらしいと思えるでしょう．もっとも，この原理がどこまで通用するか，ということに関して疑問に思っている人も居るとか居ないとか・・・

では雑文失礼．．

等重率の原理と各種物理の確率解釈

nadja さんのレス (2005/02/17(Thu) 09:37)

今までの議論で解決しているみたいですけど，ちょっと自分と理解が違うと思って書きます．王道ではない解説なので軽く読む程度にしてください．

まず「等重率の原理」とはこうでした．

ある自然現象（またはそれに準ずるおもちゃモデルなど）を，観測しているとします．その対象を物理ではよく「系」というのでここでもそれっぽく使いましょう．そして，それを解析する微視的なモデルを考えましょう．古典でも量子でも何でもいいです．そのときその系を特徴付ける微視的状態が複数あるとします．不幸にも人類の分解能では，巨視的にはそれらは区別できません． どうしましょう？困ったことになりましたねぇ． それなら特別区別することができないのだから無理に少数系の古典・量子の「力学」を推し進めるのではなく，ここらでパラダイムチェンジしてみましょう．その系をラベリングするためにちょうど少数系の「力学」でも使われている「エネルギー」を採用することにし，それを使って特徴づけてみましょう．あくまである性質を示すものをひとまとまりとして考えるのです．その系のエネルギーが同一な微視的な状態に対しては同等に扱いましょう．そういう要請です．はい，できあがり，「統計力学」の誕生です．ちょうど巨視的な物理量だけで系を記述するのに成功していた経験則「熱力学」と相性よくつなげることができることにも成功しました．めでたし，めでたし．

これが「等重率の原理」です．

ミクロカノニカルアンサンブル(N,E,V)の概念から拡張する際に，カノニカルアンサンブル(N,T,V)の概念は，あるウエート付き 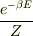$\frac{e^{-\beta E}}{Z}$ の足し合わせだったことを思い出すと，上の解説からもスムーズに理解できるとおもいます．どうでしょうか？

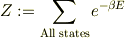
$Z:=\sum_{\text{All\ states}}e^{-\beta E}$

それよりも実はここからが本題なのですが，上での理解の違いがあると思ったのは物理の中にでる「確率解釈」の部分です．たぶんなのですが，量子力学に出てくる「量子力学的確率解釈」と統計力学に出てくる「統計力学的確率解釈」は別物です．

ここで唐突ですが，「確率・統計」というものを知っていますか？

「確率」とは高校でも習っている，さいころの各目が出る確率が 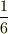$\frac{1}{6}$ ，コインの表が出る確率が 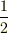$\frac{1}{2}$ というように，この確率は試行回数無限大の極限の理論値，収束値として定義していましたね．また「統計」とは心理学の実験や交差点でカウンター「カチカチッ！」することをイメージするといいですよね．そう，天気予報で出てくる降水確率も「統計」にはいりますね．

つまり，，，，，

「量子力学的確率解釈」とは（数学的厳密ではない）のですが，「確率」に，「統計力学的確率解釈」とは同様に「統計」に対応すると考えることができます．

これらのイメージとしては，「確率」とは，数学の分野の「確率論」というもので，それは「ルベーク測度」を基礎にしているもので，ある集合に対して面積（実数）を割り当てる，物理でのフーリエ変換とかにも通じる分野であり，そこでは公理論的に「確率」を定義して話を進めている数学です．それは上の試行回数無限大の極限の理論値，収束値と対応するように工夫して作っています．それに対して「統計」とは，上の例のように鈍臭く数え上げていって，その観測量を出力する確率分布（バックグラウンド，ブラックボックス）を推理するということをしているのです．「統計」ではその確率分布の推理するときに使う道具として「ベイズの公式」というものがあり，その公式には「事前確率」というものが必要になってきます．式だけ書くとこんな感じです．

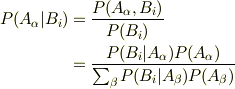
$P(A_\alpha|B_i)&=\frac{P(A_\alpha,B_i)}{P(B_i)}\\&=\frac{P(B_i|A_\alpha)P(A_\alpha)}{\sum_\beta P(B_i|A_\beta)P(A_\beta)}$

実はその事前確率 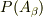$P(A_\beta)$ をどう設定するかの任意性があり，少々難しいところもありますが，物理との関係で解説しているものとして，「ベイズ統計と統計物理，伊庭幸人著」

http://www.ism.ac.jp/~iba/iwaPDF/fuku.res4.pdf

というものがあるので参照して見てください．それかもしくは同題名の岩波の文庫本も参照すると理論物理屋さん目指している人にはいいと思います．なぜなら現在の物理の研究対象の王道はほとんど「複雑な多体問題」につながっているのですから，，，，本題に戻して，

このように考えると上で議論している「量子力学上での確率」と「等重率の原理」はすぐには結びつかないような気がしますが，皆さんはどう考えますか？

ちなみに僕の専攻している分野が物理，特に統計力学のあるモデル，Isingモデルを使った確率的情報処理，平均場理論との枠組みが似ている人工知能分野の「確率伝播法(BP)」の数理的類似性を使ったアルゴリズムを主に研究しているので，上の解説は，物理一般を専攻している「物理屋」の理解とは少し違うかもしれませんので，このあとに正統な物理屋サンの解説もあると便利ですね．

では，

Re: 等重率の原理と各種物理の確率解釈

peppermint さんのレス (2005/02/17(Thu) 14:33)

なるほどー．なんか質問者でもないのに返信しちゃっても良いのかなぁ？というか僕に突っ込まれているのかとビクビクなんですが（笑

>「量子力学的確率解釈」とは（数学的厳密ではない）のですが，「確率」に， >「統計力学的確率解釈」とは同様に「統計」に対応すると考えることができます．

えーと，まず，巨大な系の微視的状態は一つ一つその出現を（完全に）観測できません．出来てたら何の苦労も要らないわけで…故に鈍臭く数えられないわけです．そこで，ある微視的な観測値（量子力学の（ってつけると変か？）固有状態）の出現"確率"を全て一緒に考えると平衡状態で上手く行くよねって事かと．ある固有状態の出現"確率"は量子力学の学問体系を作り上げる際に仮定（定義）されてるかと．そして等重率を根拠づけるのがエルゴード性かと思います．ここまでの論議では"確率"しか使っていないと思うんですが…

microcanonical ensemble はまさに等重率の原理そのままですね．そしてcanonical ensemble は・・・「canonical ensemble とmicrocanonical ensemble は熱力学的極限では（条件が同じ状態で）等しい」というのが証明できます．勿論，nadjaさんの様な"統計"のイメージで構わないと思います．ただ，その際そのガウス分布の幅は大体 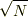$\sqrt{N}$ だと言うことです．もの凄い鋭い幅ですね．

あー，ここからは等重率の原理から逸れますが．我々の理論は，理論でしかありません．それを自然が認めてくれない限りは．物理学において純粋数学的に"確率"を定義したとしても，それを検証するには統計的手法しか有りません．だから，理論の中に"確率"が導入されていても，それは結局統計量に置き換わってしまいます．ということかと．

なんか，こうやって考えてると普段考えてないようなことまで思いついてなんかすっきりしますねぇ（俺だけ？）

あ，このＨＰは最近見つけてお気に入りです．特に悪あがき日記が（笑

追記1:なんか見返したら偉そう，且つわけわからないですね．そんなつもりはなかったんです--; 追記2:ベイズさん，難しいですね…

Re: 等重率の原理と各種物理の確率解釈

nadja さんのレス (2005/02/19(Sat) 01:21)

peppermintさんのコメントに気づいた点を少々，

まず

「巨大な系の微視的状態は一つ一つその出現を（完全に）観測できません．出来てたら何の苦労も要らないわけで…」

これは自分の解釈だと，厳密にはハミルトニアンが立てられた時点で，解析的に解くことができないだけで，たかだか 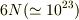$6N(\simeq10^{23})$ 個程度の物理量の非線形連立方程式を解けばいいので，苦労はさほどしませんよ．しかしその 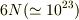$6N(\simeq10^{23})$ 個程度の物理量から有益な情報を読み取ることになると苦労かもしれません．なんせ6N次元の位相空間（phase space,,,,not toporogical）上の点（代表点），もしくはtrajectoryで自然現象を表現しようと思うと，各時刻での「情報量」が大きすぎて，有用なモデルとはいいきれません．ちなみに情報量の定義は幾通りかの流儀があるのですが，Shannon流だと，確率空間上のある集合，事象の生成確率がpであり，その自己情報量Iは

$I:=-\ln p$

と定義します．これと物理のミクロカノニカルの状態数WのBoltzmann流エントロピーの定義

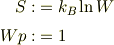
$S:&=k_B\ln W\\Wp:&=1$

に対応しています．そしてたぶんその代表点に確率を対応させるとたちまち意味のないものになっていしまいます．「自然科学」としては意味の持たないものになってはこまります．そんなことはいやですよねぇ．どうするほうがいいのでしょうか？

次に，

「ある微視的な観測値（量子力学の（ってつけると変か？）固有状態）の出現"確率"を全て一緒に考えると平衡状態で上手く行くよねって事かと，，，」

ちがいます，上で解説したとおり，観測量（ここではある特定の物理量）で系を表現しようとするモデル上で，「効果が一緒だから大して意味を持たないような細分化の必要はなし！」の方針で自然現象と物理モデル（made in human?）を漸近させているのでこのように考えるほうが無難だと思いますよ．それとその後の「量子的確率」と「統計的確率」を無理につなげようとするのは危険なのでやめておいたほうがいいです．漸近的な挙動に対して，たとえば対象が低温のFermi系になるようなところで整合性をあわせるようにすればいいだけで，あくまで「確率」と「統計」の関係でそっとしておいてやってください．お願いします．古典力学には「波動関数」なるものが存在していないと考えられているように，，，人類の分解能の精度のせいです，許してください．

細かいのだと，

もし「ガウス分布の幅」を「分散」と捕らえているのなら 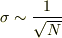$\sigma\sim\frac{1}{\sqrt{N}}$ のような気がしますが，，鋭くするために，，，

最後に，

「理論の中に"確率"が導入されていても，それは結局統計量に置き換わってしまいます．」

モデルはモデルのまま，数学のように人類が理解できる範囲内の論理性で「ごりごり」進めればいいだけで，でも究極的には「自然を解明したい」のであれば，そこでの整合性の合わせるための工夫も必要になってくるのでしょう．だから仮定然り，原理然り，だったのです．そう考えると物理って面白いですね．

おまけで，

厳密には含まないパラダイムチェンジ（古典力学VS量子力学など）や，それを含む形のチェンジ（地板構造論inプレートテクトニクスinプリュームテクトニクスなど）のように現象を観測する物理量の分解能の精度によって，概念を拡張する方法はいろいろあるように，それらの整合性（連続接続）の検証方法もいろいろあると思います．

そのような分野（数学チックにいえば，物理学基礎論？）は面白いと思います．

では

Re: 等重率の原理と各種物理の確率解釈

おこめさんのレス (2005/02/19(Sat) 02:20)

学部新３年の田舎学生その１の観点からものを言わせていただきます．全文は読んでいないので見当違いの事を書くかもしれませんがそれは許してください．

>nadjaさん＞peppermintさんのコメントに気づいた点を少々，

＞まず

＞「巨大な系の微視的状態は一つ一つその出現を（完全に）観測できません．出来＞てたら何の苦労も要らないわけで…」

＞これは自分の解釈だと，厳密にはハミルトニアンが立てられた時点で，解析的に＞解くことができないだけで，たかだか個程度の物理量の非線形連立方程式を解け＞ばいいので，苦労はさほどしませんよ．

peppermintさんのコメントは全体の印象から言うと量子力学の不確定性について言及しているように思います．それに対してnadjaさんはハミルトニアンが現実を厳密に観察した結果だと仰っているわけです．ハミルトニアンの厳密解が厳密な世界を描いているとは僕は思いません．ですが，統計力学の考え方ではnadjaさんが書き込んで下さったような数学的に定義（仮定）したもとでの計算によってある程度十分な精度で近似解が得られるという事だと思います．あ，でも分解能がどうとかいう記述がありますね．結局ここの指摘は何を意味しているのでしょうか？

以下僕の憶測です．おそらくnadjaさんは量子論は原子（イオンも含めます）くらいのスケール以上になると破綻するような有効理論でしかない．だから統計的な系をそのような量子論の確率的なものと一緒にしてもらっては困る．または単純に数学的に違うんだよ．と主張されている．のどちらかだと思っています．

でもpeppermintさんの書かれている説明はよく学部生対象の講義でなされる説明です．学部生レベルでは卒業研究など特別な事情が無い限り無理に厳密な事情などしる必要も無いかなぁ〜という感じがします．僕の大学には物理学科が無いのでそのあたりのことは詳しくありませんが．

Re: 等重率の原理と各種物理の確率解釈

peppermint さんのレス (2005/02/19(Sat) 07:12)

寝る前にこの掲示板を巡回してレスが着いていたので考えちゃって眠れない^^;ということで取り敢えず数時間考えた結果を．

>nadjaさんへ

1: >「効果が一緒だから大して意味を持たないような細分化の必要はなし！」の方針 >で自然現象と物理モデル（made in human?）を漸近させている確かに，何の実験的検証も得られてないのに（多分？）個々の量子状態が確実に等確率と決め付けるのは危険ですね．でも僕自身は微視的状態間の関係性は今後の統計物理が非平衡系とか非可逆系とかに更に発展していくためにはもっとキチンとした原理の形になる必要があると思ってます．

2:「量子的確率」と「統計的確率」がどう違うのかが良くわからんです．量子的確率は単に数学的に実験結果を説明するために導入されたものだからとかですか？それなら理解できるんですが．

3:ガウス分布の幅は正に幅（大体の，いわゆる 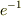$e^{-1}$ 倍になるまでの）です．分散ならそれで合ってると思います．

4:「巨大な系の微視的状態は一つ一つその出現を（完全に）観測できません．出来てたら何の苦労も要らないわけで…」って僕が言ったのは，「観測」です．「実験」でもいいですけど．実験で（勿論系に影響を与えないようにするかもしくは実験過程そのものまで系に含めるかして）一つ一つの微視的状態がどれくらいの（こっちは統計的？）確率で出現するのかわかったらこんな事想像する必要ありませんよねって事です．

5:代表点に普通に割り当てられると思うんですけど・・・だめになる理由がわからないです^^;

6:因みに僕は自然界は究極的には何らかの基本的な決まりだけで成り立ってると考えてます（そういいながら脳理論志望ですが（ぇ）．それで複雑性が理解できるとは到底思えませんけどね．．．ごりごりやるしかないんでしょうか（笑

7:たぶん，皆は物理基礎論とかやってるよりもやりたいことが沢山あるんでしょう（笑

>おこめさん

>peppermintさんのコメントは全体の印象から言うと量子力学の不確定性について >言及しているように思います．すいません，特にそれについては触れてません・・・もしそれについていうならphase spaceで 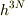$h^{3N}$ 程度の"箱"の中では我々は状態を区別できないのでこれを1状態と数える，とか．これは今回のお話とはあんま関係がないのでというか僕も良くわからんのでこれで^^;

>量子論は原子（イオンも含めます）くらいのスケール以上になると破綻するよう >な有効理論でしかないいやいや．破綻しないように量子力学の体系を作ってます．いわゆる対応原理ってやつだと思います．多分多くの物理学者はこの様な極限操作（量子論→古典論,相対性→古典系など）が成立するものを求めてると思います．これは我々の物理学的世界が必ず統一的に理解されるはずだというのを満足させる為に頑張っているんです．多分．そうでないとしてもその方が自然な拡張ですし．

>単純に数学的に違うんだよ．と主張されている．のどちらかだと思っています．ぼくはどっちかというとその学問体系の根幹をなすものを見失ってはいけないよ〜といっているのかと思いましたがどうなんでしょうね．

>でもpeppermintさんの書かれている説明はよく学部生対象の講義でなされる説明 >です．そんな，未熟さをばらさないでください（笑）僕の受けた講義ではリュウビルの定理とエルゴード性から引っ張ってきてました．

因みに久保亮五さんも「精密科学を誇る物理学の中で，しかもその重要な基礎の一つである統計力学が，それ自身どんな基礎に立っているのか良くわからない」と言っております（笑）その後に問題はどうやって等重率の原理を根拠付けるかにある，とも言っております．いやいや，この問題はそんなに簡単ではないと言うことで・・・

Re: 等重率の原理と各種物理の確率解釈

おこめさんのレス (2005/02/19(Sat) 07:58)

＞>量子論は原子（イオンも含めます）くらいのスケール以上になると破綻するよう＞>な有効理論でしかない＞いやいや．破綻しないように量子力学の体系を作ってます．いわゆる対応原理っ＞てやつだと思います．

そうですか．破綻しないような要請を課しているのは僕は知りませんでした．

to おこめ＆peppermint

nadja さんのレス (2005/02/22(Tue) 03:50)

「ハミルトニアンが現実を厳密に観察した結果」であるわけではないですよね．物理の世界では「自然現象を解明する」という目的が第１原理としてあり，その現象を忠実に表現するための「数理的な道具」として，ハミルトンのような概念の導入しているだけで，「ハミルトニアンの厳密解が厳密な世界を描いているとは僕は思いません．」というのは「宗教うんぬん」と同じで，「信じる？信じない？」の違いでしかないのですからそこの所は強制はしません．たとえば現実には誰も見たことのない「質点という概念」で「古典力学」を形成しているのをみなさんは疑わずに「信仰した」ようにすればいいのです．

ここで語弊のないように説明しますが，このような学問のもっていき方を「公理論的」というらしいです．数学チックな表現ですが，これは「数学の学問をおっぱじめる」時によく使うやり方だそうです．考えられる対象の空間（ここでは問題空間？）が広すぎる場合，その一部を規定する，問題のピントを絞る際に，使う用語は「未定義で使ってもいい」，という論法のやり方だそうです．国語辞典の用語をどこまでも原点に戻って読もうと思っても際限なくループ状態になる可能性があるので，ある程度の「用語」は決めて，「これについては言及しないで使用してよいよぉーん！」というモノを使って理論を構築しましょうってことです．だから「古典力学」は「公理論的」な枠組みで構成され，逆に「電磁気」は「逆の用語の定義，概念のもっていき方」になっていると思います．

次に「量子の枠組み」と「統計の枠組み」が数学的な性質（数理的構造）がちがうので無理に混同して覚える必要はないですよ．ホント無理しなくていいですからねぇ．これはたとえば「サイコロの確率と降水量の確率の意味は違う！」と覚えるといいですよ．実は僕はあまり授業をまじめに受けていないので，「おこめ」さんのように「教員」が嘘を教えているとは考えにくい，判断材料がなくて何とも言えませんが，今現在市販されている「大学で扱う物理関係の本」の中では，「そのような混同した確率」の解釈の使い方は一つも見あたらなかったと思います．これはまだ僕がその「変な解釈」に遭遇できない「不幸な境遇」にあるのかもしれませんが，，，彼ら「教員」はその違いは「当たり前のことは教えてどうする？知っていて当然！」と思っているとおもいます．ここについては多くは言及しませんが，この「かれら」とは今まであった名古屋大学の教員ほか，各種の研究会に参加されている

方々も含みます．厳密にはこれらは「正統物理の学会」ではなく，応用系であるということもあるのですが，，，，やっている母集団は同じですのでおんなじことでしょう，あしからず．

量子的確率は単に数学的に実験結果を説明するために導入されたものだからとかですか？

そうですね，僕の理解しているところでもそのように「量子力学的確率」を導入していました．「自然との整合性」という要請の元に導入された「不確定性原理」も誤差を表現するために導入しているみたいなところがあり，「実験機材の分解能，精度」と密接な関係があることですね．そのような理解で正しいと思います．

代表点の解釈は，考えやすいように系を表現する位相空間上を適度に微少体積に分割して離散化し，その一つ一つに確率を割り振ることにします，規格化も忘れずにしておいてくださいね．そのときある時刻tにある微少体積 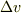$\Delta v$ に系が存在したとしましょう．一つ一つの微少体積に割り振られた確率は非常に小さいので以前紹介したか情報量

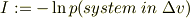
$I:=-\ln p(system\ in\ \Delta v)$

は下に凸でなおかつ $p\to0$ の極限で発散してしまうことが分かると思います．これは系を観測するという目的がある我ら地球人にとっては意味のないことです．違う電波系の方々には意味のあることになるのかぁ，，うぅんわからんのでコメント控えましょう．

関係ないかもしれませんが，情報系では「アナログ信号からデジタル信号」に変換することを「量子化（Quantization）」というそうです．全く意味ないトレビアですねぇ，，，，

「自然界は究極的には何らかの基本的な決まりだけで成り立ってると考えてます」大いにいいことだと思います．僕もそう思います．しかしそれは往々にして人類が理解できない（性能がまだまだ低いので）形で存在しているのでしょう．もしかしたら今も目の前にあるのに見えていないかも，，まぁ現在の「そう言う関係を研究している分野，素核宇宙」にパラダイムチェンジがない限りは無理でしょう．口で言うのは簡単なのですが，「人類の側からたった自然の捉え方」ではなく「もっと高次の違う立場に立った上での自然の捉え方」にしないとだめでしょうね．このいっている意味の捉え方はいろいろあると思いますのでいろんな風に解釈してください．そうですね，自然の「気持ち」を理解するまではまだまだ長い道のりがあるようですね．

「脳理論志望」お，これはいいところに着目したと思います．これは個人的な意見ですが，現在ある分野に多額のお金をつぎ込んででた結果が「やっと教科書一行」という「ばかげた税金の使い方はよくない（まぁ敵をつくるような表現ですこと）」という流れがあり，それではいけないだろうということで，現在国の政策は「より国民の生活が豊かになる，ためになる」ような学術を戦略的に押し進めているようです．ちまたで「なのなの」ゆうてもてはやされているのもそのためです．ちなみに僕個人は「出されたモノをこなせるだけの性能のいい，賢い」人間（マシーン）よりは「将来を見据えた先験的になれるずるがしこさを持った」人間（マシーン）のほうが上に立つといろんな成功している人を見て思います．研究者を目指すなら，何を研究するべきかの判断できるのは，最低限必要な条件なのでしょう．（くどい様ですが，それで十分とは言えませんがね）

物理関係でおもしろそうなモノをいえば，「経済物理学」なんてのはどうですか？大きく分けて「金融工学（物理でいう経路積分なんかが使われている）」，「ゲーム理論（統計力学の考えが使われているMinority Gameとか）」とその他があり，物理的なモノの見方が適用できる部分と適用できない部分があり，たくさんの仕事が残っている分野なのでここ１０年で研究職に就こうと考えているなら格好の参入場所ではないでしょうか？そのためには人の何倍の分野を網羅する覚悟があればですけど，，

以上，これらは僕の個人的な意見なのであまり参考にはならないと思いますが，おこめさん，peppermintさん，そのほかのみなさんどう思われますか，返信待っています．

では，

Re: to おこめ＆peppermint

おこめさんのレス (2005/02/22(Tue) 14:42)

>実は僕はあまり授業をまじめに受けていないので，「おこめ」さんのように「教員」 >が嘘を教えているとは考えにくい

僕の大学での学部生レベルの講義では必要に応じて，いくらでもごまかしの説明をしますよ．ただしそれは多くの場合，少し調べれば気づく事です．その段階ではそのように思ったほうが"親しみやすい"，"面食らって拒絶することを防ぐ"などの狙いがあるように思います．これとは別件ですが，そういう狙いで説明しているんだとの返事がもらえた経験があります．

僕の大学の99%以上の学生は卒業後に，物理に全く関係のない仕事につこうとしているので，そのように教える方が良いんだろうなぁと勝手に思っております．

統計力学，量子力学については全く勉強していない（統計は講義を聞いただけ，量子は演習だけ）ので，専門家の方の意見が聞けて良かったです．希望のある意見が聞けて，物理の世界とは関係の無い（この世にいる限り関係してはいますが）僕も元気が出てきました．

Re: to おこめ＆peppermint

おこめさんのレス (2005/02/22(Tue) 14:54)

>「ハミルトニアンが現実を厳密に観察した結果」であるわけではないですよね．物 >理の世界では「自然現象を解明する」という目的が第１原理としてあり，その現象 >を忠実に表現するための「数理的な道具」として，ハミルトンのような概念の導入 >しているだけで，「ハミルトニアンの厳密解が厳密な世界を描いているとは僕は思いません．」というのは「宗教うんぬん」と同じで，「信じる？信じない？」の違い >でしかないのですからそこの所は強制はしません．たとえば現実には誰も見たこと >のない「質点という概念」で「古典力学」を形成しているのをみなさんは疑わずに >「信仰した」ようにすればいいのです．

宗教ですか，すみませんでした．僕は上に書かれているような意味で，「ハミルトニアンの厳密解が厳密な世界を描いているとは僕は思いません．」と書いたのですが，全く伝わらなかったようです．僕は文章で何か意味のある事を書く自信は無いので，これで失礼します．

[home] [掲示板] [ページの先頭]