無題

和尚人さんの書込 (2005/02/10(Thu) 12:29)

物理数学の内容を見せていただきました．とても楽しいお話で勉強になりました．そのとき，ガウス積分のお話に興味を持ったのですが，小生は数学が苦手なもので以下の箇所のイメージがつきにくかったです．＞ここで x = r sin theta ， y = r cos theta と変数変換をします．なぜここでこのようなことをするのかがイメージできません．＞また，無限遠で積分領域を矩形から円形へと変形します．被積分関数が無限遠で速やかに0に収束することから，このようにしても積分値は変わりません．すると (3) 式は，ここでおっしゃっていることもイメージしにくいです(私にとっては)．

もし，よろしければ，簡単にご教授していただければうれしいです．宜しくお願いいたします．

Re: 無題

おこめさんのレス (2005/02/10(Thu) 14:58)

上に書かれていることは計算を可能にするテクニックだと思っていただいたらいいと思います（なぜこのような操作が有効なのかは説明できません．）．

後イメージの方はある場所を中心に小さな山があります．その山の高さはあるところ以降は殆んどゼロに近い値を取ります．このときに無限遠まで積分するわけですが，その果て（果ては実際にはありません）の形が矩形だろうが，円形だろうが足した量（積分値）は変わらないということです．なぜ量を無限に足しているのに有限の値に落ち着くのかもついでに書いておきます．話のすり替えになってしまうかもしれませんが例えばX＜１という量は無限の和となります．具体的には X=0.9+0.09+0.009+0.0009+・・・=Σn=0,∞(1/10)^n*0.9 という∞の和になるのです．積分の場合はこれが連続変数になるというイメージです．

イメージなどで説明をすると話が厳密でなくなりますし，自分の認識も甘い（物理をする上では困りませんが）ので詳しい方が後で説明を加えたり，修正されると思うので鵜呑みにせず，参考までにしてください．物理は数学で無いので極端な話，公式を丸覚えしていてもさほど困らないんですけどね．使うべきときにいつもその公式が思い出せればとりあえずOKという感じです（使いどころを把握する方が何倍も重要です）．

ガウス積分の公式

CO さんのレス (2005/02/10(Thu) 15:30)

和尚人さん，こんにちは．

>> ここで x = r sin theta ， y = r cos theta と変数変換をします． > なぜここでこのようなことをするのかがイメージできません．

まず，元の積分が

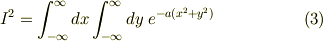
$I^2 & = \int_{-\infty}^{\infty} dx \int_{-\infty}^{\infty} dy \ e^{- a (x^2 + y^2)} \tag{3}$

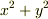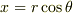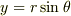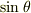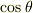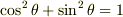でした．ここで， x^2 + y^2 という形に注目します．この形がでてきたら， $x = r \cos \theta$ ， $y = r \sin \theta$ と置換するのが定石です．（はっ，記事中では $\sin \theta$ と $\cos \theta$ が逆でしたね (--; ) なぜかというと， $\cos^2 \theta + \sin^2 \theta = 1$ という関係，および 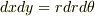$dx dy = r dr d\theta$ という関係があるからです(これは高校の数学で習いますよね)．この関係を使えば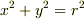， x^2 + y^2 = r^2 となり，被積分関数が $\theta$ には依らない，事実上の一変数関数の積分に変換できることがわかるからです．つまり，

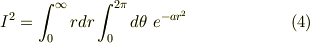
$I^2 & = \int_0^{\infty} r dr \int_0^{2\pi} d\theta \ e^{-a r^2} \tag{4}$

のようになるわけですね．被積分関数に $\theta$ は含まれませんので， $\theta$ についてはただちに積分できてしまいます．

Re: ガウス積分の公式

おこめさんのレス (2005/02/10(Thu) 15:38)

値の分布が上下左右に対称（正しい表現かはわかりません．円対称？）なので極座標で積分するのが簡単に計算を実行する有効な方法だとパッと思いつくと思います．これは電磁気などで球対称な電場を積分するときに球座標を使うなど経験的に演習を積めば身についていく感覚です．全然理由の説明などにはなっていませんが・・・

[home] [掲示板] [ページの先頭]